Back to previous page
Discovering governing equations from data by sparse identification of nonlinear dynamical systems, PNAS April 12, 2016 113 (15) 3932-3937; https://doi.org/10.1073/pnas.1517384113
What do you think about this paper?
The paper is very well written, with persuasive real-life examples and an honest commentary on when it is and isn't likely to be successful. It seems to be an ideal assembly of sparse regression methods and POD methods to advance a different and important application area (nonlinear dynamical systems).
-----
As far as I can gather (I saw this paper some time ago) the technique doesn't generate a mechanistic model but state equations that are a combination of constants, polynomials, and trig terms. It's a technique for fitting generalized equations, akin to a neural network (in principle, not exactly the same). Furthermore, it requires time series data on all states in the system which one may or may not have. I don't think they indicate how the resolution of the time series data affects the outcome but they do add noise to the time series data. The fact that the technique doesn't generate a mechanistic model is a negative for me. As the authors point out there are a number of related methods but they don't scale well. It is interesting that the model they chose to serve as an example only has three state variables and whose state equations contain first-order terms. This isn't a particularly demanding example, yes its chaotic but I don't think that's a significant issue. For a signaling pathway, we might be dealing with 50 states and the equations could have any structure. We really need to rethink how we develop models of cellular function.
We're developing an alternative approach that does generate mechanistic models from experimental data using a machine learning technique and we think it scales. Our technique does not require time series data but can use if it is available. If states are missing (which is highly likely) our technique will give alternative models that satisfy the limited data that is available.
It might be worth trying their technique on a biochemical model such as a signaling pathway but even if it did manage to generate a mechanistic model from raw data (which I don't think it can since it is based on polynomials and trig functions, plus the required time series data simply isn't available) it still doesn't address one of the main sources of uncertainty which is the model itself. This is something we do address.
Herbert Sauro
---------
Thank you both for the feedback.
Herbert, I really like your suggestion of trying to "close-loop" the two models to see if they generate consistent results. In the mechanistic modeling world (e.g., biophysically-realistic models of neurons) the equations we write are biased by our theories. Basically, we select what are the features of the data that matter and we write those equations. In this paper the equations unbiasedly arise from the data. Of course this is not truly unbiased (e.g., we select: the units of analysis, the spatial/temporal resolution, because we believe those are appropriate, etc.,). The reason why I think this is interesting is because once you have the equation(s) we can test where those parameters and operations are reppresented in the brain. We could even do a synthetic "controllability study" to test what is worth manipulating in future causal interventions and that would be more mechanistic in my view. I believe this study goes beyond dimensionality reduction and features extraction, and it's completely explainable (i.e., not a "black box"). Does this make sense?
Michele Ferrante
--------
Michael, I looked again at their paper and this time at their supplement. It turns out they do try their method on a model of glycolysis which is more relevant to me. What is interesting is that they find for those states that include rational functions eg k1 S1 S6/(1 + (S6/K1)^q), the method fails to capture the dynamics for those particular states. Rational functions are common in biochemical networks. This shows that their basis functions: polynomials and trig functions are probably not sufficient. Plus I don't think they actually recreate the original model just something that behaves like the original model (except for those states that were determined by rational functions). It is useful that they can capture the dynamics, however. There is another group I know that did something similar, I should dig up their published work. For a mechanism person such as myself, their approach, though interesting and thought-provoking, doesn't help the likes of me. From a biomedical point of view, I feel we must have mechanistic models because our therapies target mechanisms. At this point in time, I'm not convinced it's not a black box they are creating. I spoke to one of the group over a year ago and they said that what they getting are 'empirically' derived functions that match the measured dynamics. However, I could be wrong and should go back to talk to them. I am still interested in your comment that you don't think its a black box as I didn't quite follow your argument. eg I didn't quite follow your statement: 'we can test where those parameters and operations are reppresented in the brain.'
As I mentioned before we're developing a completely different approach that will generate mechanistic models. I don't want to say much about it here but would be happy to explain it to you if you're interested and the philosophy behind it.
Herbert Sauro
------------
Thanks Grace, for sending out the link and thanks Michele for bringing the paper to Grace's attention. I'm familiar with this paper, as well as its References 3 and 4; addresssing my perceived limitations of that work is in fact the motivation for our newly funded UO1 (shameless self-promotion...). My own perspective is much more in line with that which Herbert presented in his comments: I am more bio-mechanism oriented. To be more explicit, I am focused on the behaviors/controls of biomolecular pathways than representing biological systems as physio-mechanical systems, with the added "multi-scale" aspect that it is not just biochemical pathways (let's call this "microstates") but how those pathways manifest as encapsulated in cells that exist as populations in tissues/organs, and that the manifestation of "disease" from a clnical level is dysfuction of those tissues/organs (let's call this "macrostate"). As such, I would claim that one of the core assumptions of this paper, reflected in the sentence: "In particular, we leverage the fact that most physical systems have only a few relevant terms [emphasis mine] that define the dynamics, making the governing equations sparse in a high-dimensional nonlinear function space." does not in fact hold for the representations that underpin most pharmocological development, e.g. finding compounds that interact with pathways (microstate) operating in the multi-scale context of tissues/organs/organisms (macrostate). In addition to echoing Herbert's comment above that this paper's approach of equation fitting (applicable for the examples presented that are known to be governed by a defined and limited set of equations) does not provide the bio-mechanism-level granularity needed to engineer controls/therapies, I also think that the representational form; that of deterministic non-linear dynamical systems, is not quite correct, namely because of how it treats (or more correctly, doesn't treat) stochasticity. In the method described, "noise" is a property of the data, not of the mathematical representation per se; the approach seeks to "fit" the noise in the data into a determinstic representation, and in so doing treats that noise as a term that is meant to be reduced rather than an intrinsic component of the system; in essence substituting deterministic chaos for stochasticity. Alternatively, for biological systems (at least at the top tier macrostate of the multi-scale hierarchy), that stochasticity is a feature of the generative dynamics of those systems, responsible not only for heterogeneity of behaviors/trajectories of biological systems but also the lack of microstate path-uniqueness to any specific macrostate of the system (both robustness features of biology necessary for evolution to function). Therefore, any representations based on deterministic dynamical systems (and associated formal concepts of bifurcations and attractors) are insufficient when trying to bridge the scales between molecular interactions to tissue/organ function (I leave out discussion of the brain, about which I know nothing about). Futhermore, since drug/control/therapy discovery nearly invariably operates at the microstate level (mediators/pathways), to use the method presented requires fairly extensive time series data on microstates (as they relate to macrostates), and the scale of that data is grossly insufficient given the degrees of freedom presented by the number of components/vectors needed for microstate characterization. This leads to my perpetual contention that, in terms of data needed for effective, generalizable machine learning, biology is data-poor. I introduce my argument for this case, as well as the role of multi-scale modeling as a remedy, in a recent perspectives article in Bulletin of Mathematical Biology (https://link.springer.com/article/10.1007/s11538-018-0497-0); if it looks familiar to some it is because the article is an expansion of the Introduction for our UO1 (which in turn is derived from a short talk I gave at the 2014 MSM Satellite Session https://www.imagwiki.nibib.nih.gov/content/msm-2014-satellite-session). Along those lines, we have pursued an approach similar to that presented in the paper, but leveraging our contention that sufficiently complex multiscale models can serve as proxy systems for real-world systems, thereby both overcoming the data-poor limitation and providing a reference point to microstate vector selection by virtue of an existing model (e.g. hypothesis structure). The goal here, however, is not that the resulting equation construct is directly relatable to the real world system, but rather it provides some insight into intermediate organizational structures of dynamic importance to aid in coarse graining the representation of the real world system (and can therefore be used for control discovery via either evolutionary computation or deep reinforcement learning -- these tasks are the goals of our UO1). To take off a bit from Michele's comment about "close-looping" the "two models" I can envision an iteration between a MSM and its derived-equation representation that can potentially converge on semi-optimal level of graining for control discovery. I would be interested in finding out more about Herbert's method of generating mechanistic models, since that is an aspect we don't directly address.
Gary An
---------
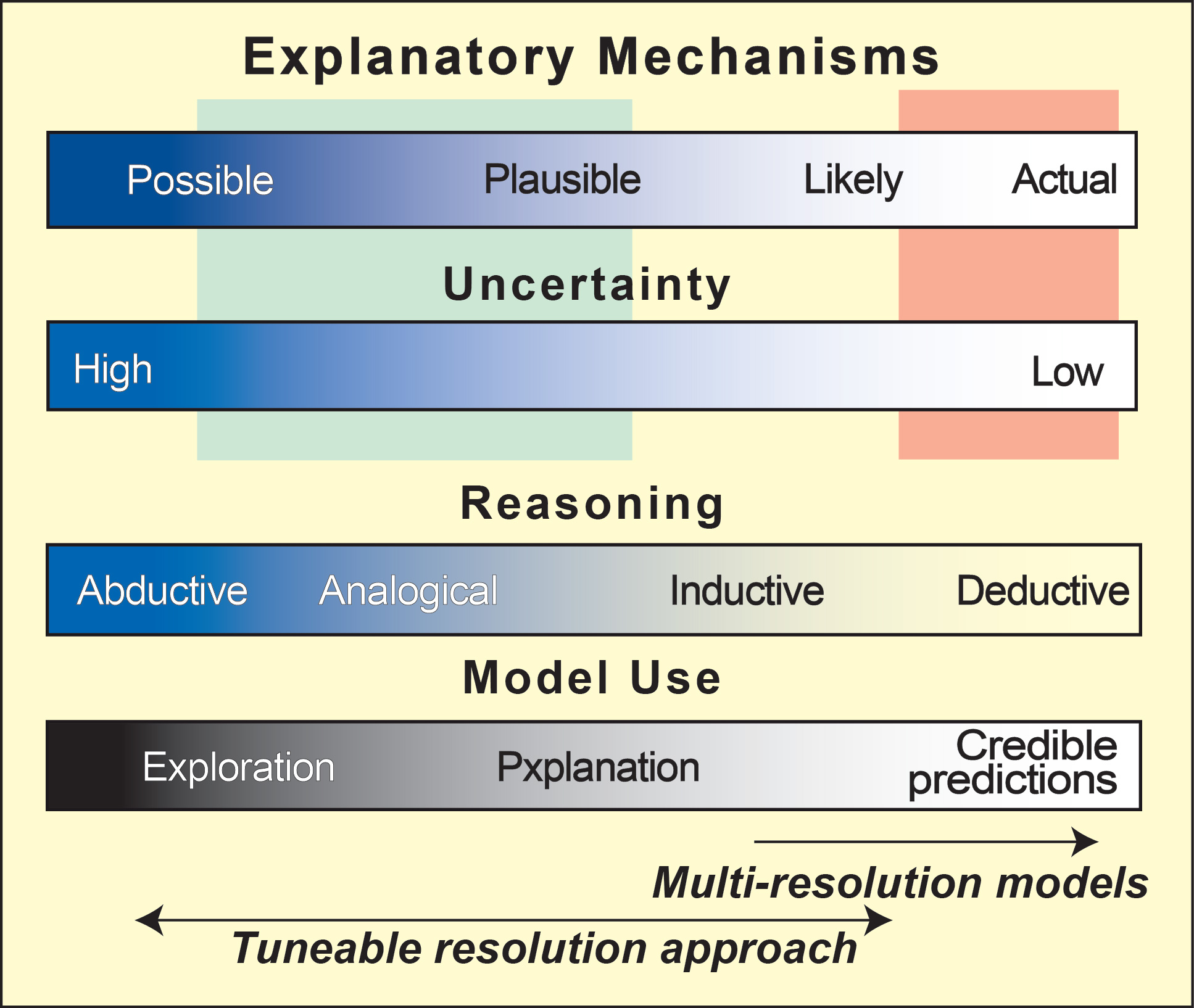
Most inductive problem-solving methods do not work well left of center on the above spectra (most living system problem lie left-of-center). But the new technique in this paper could be successful in a domain that is left-of-center, as long as the solution space is "smooth" or well-behaved.
• All of their examples are explorations of both the forward and inverse map, which is fantastic. However, MSM scientists will need to test uses of the method in situations where we really do not know that/if there is a (elegant) generative solution to the problem.
• Brunton et al. consistently use the phrase "physical system". They focus on analytic functions like polynomials, trig, and differential equations. Doing so seems to argue that the method will only work for "smooth" solution spaces. But that conjecture needs to be challenged. My guess is that it is because of the chosen example systems and, more importantly, the failures they (thankfully) list in Appendix B (choice of coordinates, choice of basis).
• I have two question that I’d like to pose to the authors.
To what extent do you believe biological systems would display the required sparse solutions, given that (large) biological systems are complex and measuring them can be quite messy?
Given that many multi-models (multi-scale, multi-formalism) are systemic compositions/integrations of smaller models (componentized or simply hacked), to what extent might this method apply to such compositions?
• There seems to be some assumption that every important variable can be addressed/modeled. Often in multi-models, a fine-grained (small and fast) set of variables generates (part of) a larger variable. And that larger variable is then used in the interaction of that component with the larger/slower variables of other components.
It is reasonable to expect that one could perform this method on each component, despite whether that is currently feasible. Doing so would result in these (polynomial, trig, DifEq) "gray box" characteristic equations. The question is, to what extent would those equations map to the underlying (finer grained) explanatory mechanisms? Will it be necessary to assume that the same formalism could apply all the way from the coarsest to the finest generative mechanism?
• I infer that their methods will work on any problem formulation (e.g., MSM) that could be solved by continuous math.
• Systems with significant discrete generative features will, I posit, bifurcate into 2 classes: those that can be approximated by solutions of this type and those (probably less consistent biology such as a system under the influence of a disease) for which this method will likely fail (systems behaviors that are less amenable to purely reductionist methods of explanation). The authors will probably agree and say that is an area for future research.
• Re: evolving dynamics, such as biological systems in which a consequence of biology-environment interactions is that the biology adapts, reengineers some critical generative mechanisms.
Brunton et al. explicitly address evolving dynamics in which the function changes over time. So, the mechanism need not be fixed. However, the 2 critical assumptions (proper coordinate system and proper basis) are not independent of things like non-stationarity. So, it seems likely that the way the dynamics evolve will matter and/or the extent to which they evolve will also matter.
• A practical technical issue: It is difficult to map the continuum math used by Brunton et al. to (purely) constructivist/intuitionist math or computer simulations. Proof assistants like Coq and Isabelle can represent intuitionistic logic. And the HoTT (Homotopy Type Theory) posits an equivalence between intuitionist and classical logic. But, a BUNCH of work will be required to transform one into the other.
• Re: biological variability, robustness, and polyphenism (incl. significant individual variability) – These issues will present problems for the method because the method itself is still purely inductive. It is not an updateable induction like Bayesian methods. So, if 2 different mechanisms generate the same behavior, the functions found by their sparse compressed sensing would (effectively) be a classifier establishing those 2 mechanisms into an equivalence class.
Polyphenism is, arguably, worse for their method because the function it would find would not completely cover/circumscribe the generators. This would (I think) be a case of over-fitting because whatever context caused the mechanism to generate this behavior vs the other behaviors it could have generated was left out of the data set from which they induced that function. Nevertheless, one can mitigate these risks. The question is, ultimately, how much manual labor does this sort of thing cost in a real reverse engineering (MSM) setting.
Anthony Hunt

