Model describing 2 compartments with osmotic water and solute exchange (no solute water interaction)

Description

 Model describing 2 compartments with osmotic water and solute exchange 
 (no solute water interaction). Models uncoupled, independent fluxes of water 
 and 2 solutes, A and B. Membrane separates 2 stirred tanks, of volumes V1 and V2,
 that have stretchable walls, rather stiff, with elastic coeff of 135.9 mmHg/ml
 means that the pressure required to add 1 ml water to the chamber, is equivalnet 
 to raising a column of Hg by 13.59 cm.  The density of mercury, Hg, is 
 rho Hg =13.59508 g/ml, so ∆p = 1 cm H20 (with density 1) = 1.359508 mm Hg.
 Solute activities are assumed to be unity.
     In the steady state, achieved in about 15 seconds in the Figure, the osmotic
 pressure counter-balances the hydrostatic pressure. Given the Van’t Hoff equation
 for a solute with an activity coefficient of 1.0:
     PI = C.R.T, 
 where PI is the osmotic pressure, C is concentration, Molar, and RT is the gas
 constant times the temperature in deg Kelvin..Using it as a test of the numerical
 solution of the differential equations, the steady state pressure difference of
 18.131 mmHg (at 45 sec to be sure) should be balanced by C.RT, which is the final
 A1 of 0.93749 mM times an RT of 19.34*10^6 mmHg.cm^3/mole.
    This gives the result 18.131 mmHg, exactly correct to 5 decimals. This model
 is a simple one, and should be accurate:  the result attests to the fidelity
 of the computation. Van’t Hoff had it right!
     This model contrasts with that of Kedem and Katchalsky (1958) in which the 
 water and solute exchange through a small pore, with opposing velocities when 
 the solute gradient provides the driving force, though it degrades if there's
 solute leakage.
  

Equations

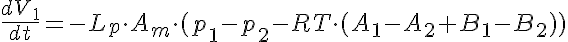
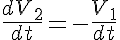
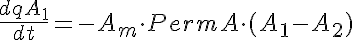
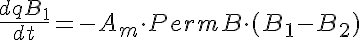
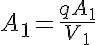
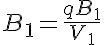
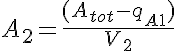
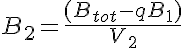
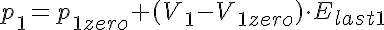
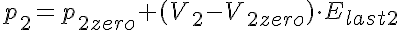
The equations for this model may be viewed by running the JSim model applet and clicking on the Source tab at the bottom left of JSim's Run Time graphical user interface. The equations are written in JSim's Mathematical Modeling Language (MML). See the Introduction to MML and the MML Reference Manual. Additional documentation for MML can be found by using the search option at the Physiome home page.