ODE model of actin polymerization and depolymerization with tracking of bound nucleotide

Description

This ordinary differential equation model describes actin 
polymerization and depolymerization with rates which depend on the 
hydrolysis state of bound nucleotide. The model accounts for the 
concentrations of monomeric actin bound to ATP, ADP-Pi, and ADP, and 
within filaments, the fraction of subunits at each location throughout 
the filament which are bound to ATP, ADP-Pi, or ADP. The identity of 
bound nucleotide is important for actin because it affects 
polymerization and depolymerization kinetics as well as the binding 
of several important binding proteins, including ADF/cofilin and 
Arp2/3 complex. The published model the current model was based on 
was the first to quantitatively identify the distribution of bound 
nucleotide along the length of actin filaments. All rate constants 
are adjustable, as are capping fractions for each end of the filament. 
The model output values include concentrations for all the nucleotide 
binding states for monomers, filament concentrations, and nucleotide 
binding state fractions for each individual subunit position throughout 
the simulated filaments. In addition, the fractions are assembled into
profile variables in order to make it easier to view complete filament
nucleotide profiles.  These profile variables (Pt,Pdpi,Pd) are functions
of two dimensions, s, which is subunit location within filaments measured
from the barbed end, and t, time. So, a plot page curve of Pt(s,100) will 
show how the fraction of subunits bound to ATP varies along the entire 
filament after 100 seconds of simulation. A plot page curve of Pt(10,t), 
on the other hand, will show how the fraction of subunits bound to ATP at 
the 10th subunit from the barbed end varies over time.
	In the JSim realization of this model, we need a fixed number of 
equations and therefore need to fix the length of the filaments we are 
simulating. If you would like to investigate filaments of a different length 
than the default for this download, this is made easier by the use of the 
MPC utility (available at imagwiki.nibib.nih.gov/physiome/jsim/models/webmodel/NSR/MPC/). 
If you are interested in this option, make sure that you download the 
ActinCycle1.mpc file for this model as well as the ActinCycle1.proj file, 
since you will need the MPC source code to generate a new model file with 
the correct number of equations for your desired filament length. 
Detailed instructions can be found in the model source code and in 
the MPC source code. Note that doubling the length of the simulated
filaments increases the simulation computation time by a factor 
of 5 to 6.

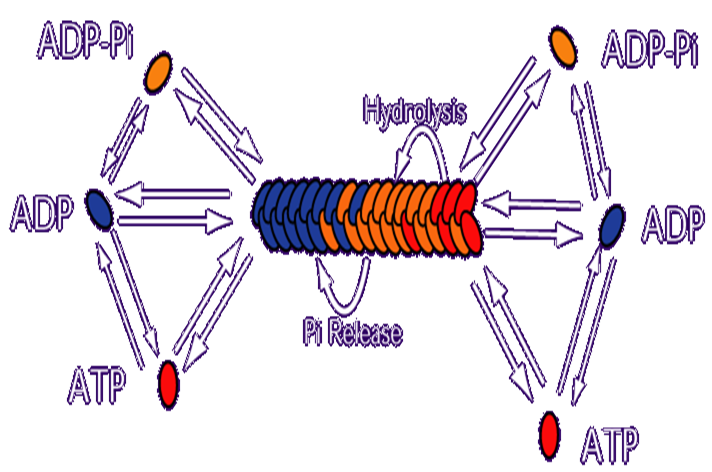
Each oval in the figure above represents an actin molecule. The color of the oval represents the state of the bound nucleotide. Red = ATP bound, Orange = ADP-Pi bound (where ATP hydrolysis has occurred, but the Phoshphate ion has not dissociated from the actin), Blue = ADP bound. On actin monomers, hydrolysis is negligible, so the primary methods of changing the state of the bound nucleotide are Pi release (which converts a monomer from ADP-Pi bound to ADP bound) and nucleotide exchange, where an actin monomer releases it's nucleotide altogether and binds a new one. In our model, we assume an excess concentration of free ATP in solution, so nucleotide exchange results in an ATP bound monomer. Monomeric actin molecules polymerize to form filaments. Filaments have two kinetically distinct ends and all lengthening or shortening of filaments occurs from subunits associating or dissociating from one of these ends. Both association and dissociation rate constants tend to be higher at one end of the filament, referred to as the "barbed" end. The other end is referred to as the "pointed" end. Once incorporated into filaments, ATP-bound actin subunits convert to ADP-Pi bound actin subunits through hydrolyzing their ATP, and ADP-Pi subunits convert to ADP-bound subunits by releasing their Pi. The ratio of on to off rates is higher at the barbed end than the pointed end, which results in this system settling into a steady state where there is net polymerization of ATP-actin at the barbed end and net depolymerization of ADP-actin at the pointed end, meaning that there is a flux of subunits moving from the barbed to the pointed end. This "treadmilling" is indirectly powered by the ATP being drawn from the surrounding solution.

Equations

ODEs governing changes in monomer concentrations:

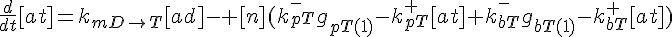
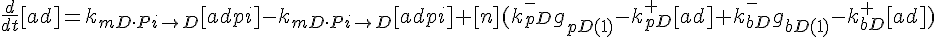
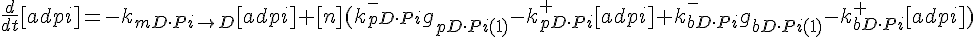
Flow into and out of filamentous pool

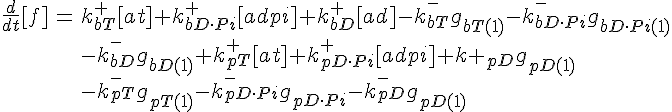
Conservation of Actin

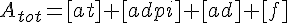
ODEs governing filament tip subunit fractions

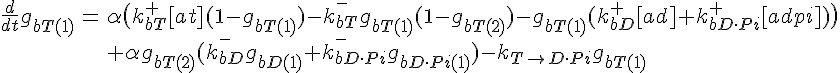
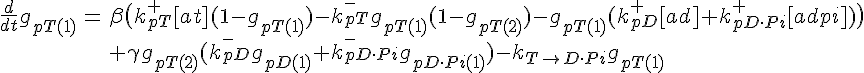
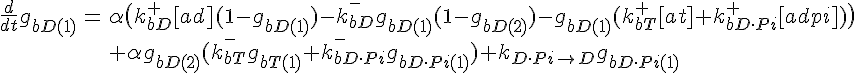
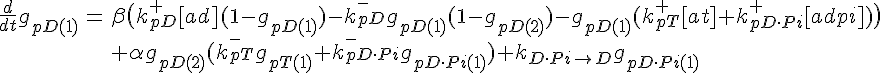
Filament tip subunit fractions must sum to one:

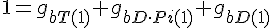
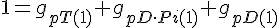
Equations governing internal subunit fractions

The following are the equations for the ith subunit from the tip, counting from the barbed end:

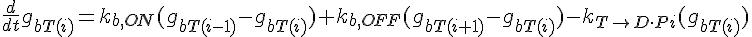
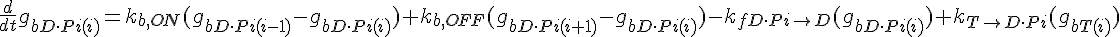
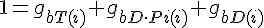
where  ,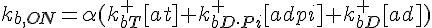 

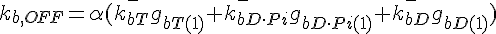
The following are the equations for the ith subunit from the tip, counting from the pointed end:

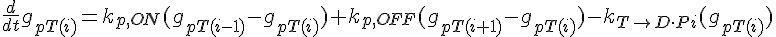
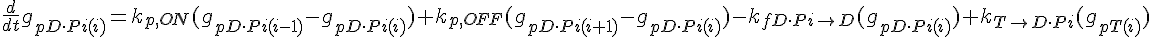
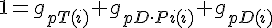
where  ,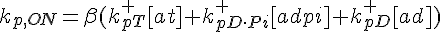 

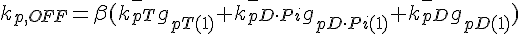
For the subunit at the exact center of the filament (designated here by location i*), we require that it lies on a cubic spline connecting subunits from the barbed and pointed end governed equations. This guarantees that the value of the profile and it's derivative vary smoothly across this center connection point.

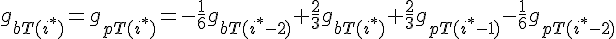
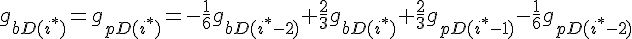
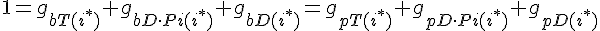
The equations for this model may be viewed by running the JSim model applet and clicking on the Source tab at the bottom left of JSim's Run Time graphical user interface. The equations are written in JSim's Mathematical Modeling Language (MML). See the Introduction to MML and the MML Reference Manual. Additional documentation for MML can be found by using the search option at the Physiome home page.