Model describing 2 compartments with osmotic water and solute exchange (no solute water interaction)
Description
Model describing 2 compartments with osmotic water and solute exchange
(no solute water interaction). Models uncoupled, independent fluxes of water
and 2 solutes, A and B. Membrane separates 2 stirred tanks, of volumes V1 and V2,
that have stretchable walls, rather stiff, with elastic coeff of 135.9 mmHg/ml
means that the pressure required to add 1 ml water to the chamber, is equivalnet
to raising a column of Hg by 13.59 cm. The density of mercury, Hg, is
rho Hg =13.59508 g/ml, so ∆p = 1 cm H20 (with density 1) = 1.359508 mm Hg.
Solute activities are assumed to be unity.
In the steady state, achieved in about 15 seconds in the Figure, the osmotic
pressure counter-balances the hydrostatic pressure. Given the Van’t Hoff equation
for a solute with an activity coefficient of 1.0:
PI = C.R.T,
where PI is the osmotic pressure, C is concentration, Molar, and RT is the gas
constant times the temperature in deg Kelvin..Using it as a test of the numerical
solution of the differential equations, the steady state pressure difference of
18.131 mmHg (at 45 sec to be sure) should be balanced by C.RT, which is the final
A1 of 0.93749 mM times an RT of 19.34*10^6 mmHg.cm^3/mole.
This gives the result 18.131 mmHg, exactly correct to 5 decimals. This model
is a simple one, and should be accurate: the result attests to the fidelity
of the computation. Van’t Hoff had it right!
This model contrasts with that of Kedem and Katchalsky (1958) in which the
water and solute exchange through a small pore, with opposing velocities when
the solute gradient provides the driving force, though it degrades if there's
solute leakage.
Equations
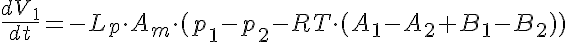
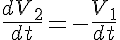
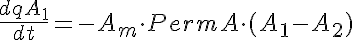
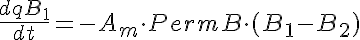
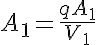
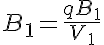
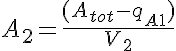
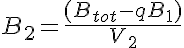
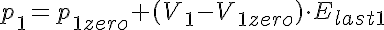
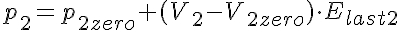
The equations for this model may be viewed by running the JSim model applet and clicking on the Source tab at the bottom left of JSim's Run Time graphical user interface. The equations are written in JSim's Mathematical Modeling Language (MML). See the Introduction to MML and the MML Reference Manual. Additional documentation for MML can be found by using the search option at the Physiome home page.
- Download JSim model MML code (text):
- Download translated SBML version of model (if available):
We welcome comments and feedback for this model. Please use the button below to send comments:
Katchalsky A and Curran PF. Nonequilibrium Thermodynamics in Biophysics.
Cambridge, MA; Harvard University Press, 1965.
Kedem O and Katchalsky A. Thermodynamic analysis of the permeability
of biological membranes to non-electrolytes. Biochim Biophys Acta 27: 229-246, 1958.
Stein WD. The Movement of Molecules across Cell Membranes. New York; Academic Press, 1967.
Stein WD. Transport and Diffusion across Cell Membranes. Orlando, Florida; Academic Press Inc., 1986.
Bassingthwaighte JB. A practical extension of hydrodynamic theory of porous transport
for hydrophilic solutes. Microcirculation 13: 111-118, 2006. (for estimating sigma and Ppore
from dimensions of solute and pore).
Please cite https://www.imagwiki.nibib.nih.gov/physiome in any publication for which this software is used and send one reprint to the address given below:
The National Simulation Resource, Director J. B. Bassingthwaighte, Department of Bioengineering, University of Washington, Seattle WA 98195-5061.
Model development and archiving support at https://www.imagwiki.nibib.nih.gov/physiome provided by the following grants: NIH U01HL122199 Analyzing the Cardiac Power Grid, 09/15/2015 - 05/31/2020, NIH/NIBIB BE08407 Software Integration, JSim and SBW 6/1/09-5/31/13; NIH/NHLBI T15 HL88516-01 Modeling for Heart, Lung and Blood: From Cell to Organ, 4/1/07-3/31/11; NSF BES-0506477 Adaptive Multi-Scale Model Simulation, 8/15/05-7/31/08; NIH/NHLBI R01 HL073598 Core 3: 3D Imaging and Computer Modeling of the Respiratory Tract, 9/1/04-8/31/09; as well as prior support from NIH/NCRR P41 RR01243 Simulation Resource in Circulatory Mass Transport and Exchange, 12/1/1980-11/30/01 and NIH/NIBIB R01 EB001973 JSim: A Simulation Analysis Platform, 3/1/02-2/28/07.

