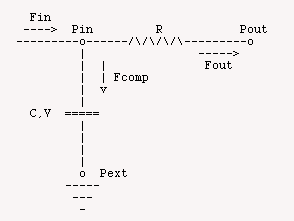
This model describes a flow through a single vessel with fixed resistance to flow, R, compliance, C, and a pressure drop along the vessel of Pin - Pout.

Description

This model simulates the flow, volume and presssure of a compliant, resistive vessel. A sinusoidal input pressure, P_in drives the flow in the vessel. This simulation employs the fluid analog of a resistive-capacitive electrical circuit where flow, F, is equivalent to electrical current, pressure, P, is equivalent to voltage, compliance, C, is equivalent to electrical capacitance, and resistance to flow, R, is equivalent to electrical resistance. The flows, F_in, F_out and F_comp, and the vessel volume, V are unknown in this simulation. Therefore the four equations given below are needed to solve for the these unknowns. A fifth equation to solve for resistance given the vessel geometry is also given below.

Equations

There are five basic equations which are used in this model. The first equation for flow out of the vessel is related to the resistance by the fluid equivalent of Ohm's Law.

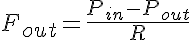
where P_out is the pressure at the outlet of the vessel and R is determined from Poiseuille's Law as:

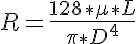
where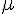is the fluid viscosity, L is the vessel length, and D is the vessel diameter.

The flow into the vessel and the flow out of the vessel are different because of the change in volume which adds or subtracts flow from that leaving the vessel depending on whether the pressure is increasing or decreasing in the vessel. So we have:

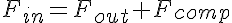
where the flow attributed to the vessel compliance, F_comp, is given by:

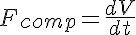
and where V is the vessel volume and is related to the compliance, C and intraluminal pressure, Pin, by:

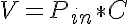
In this simulation the initial vessel volume is prescribed by Pin and C is calculated from the initial diameter and vessel length.

The equations for this model may be viewed by running the JSim model applet and clicking on the Source tab at the bottom left of JSim's Run Time graphical user interface. The equations are written in JSim's Mathematical Modeling Language (MML). See the Introduction to MML and the MML Reference Manual. Additional documentation for MML can be found by using the search option at the Physiome home page.