When flow of solute in a solution under pressure is retarded so that its flux across a membrane is slower than the solvent flux, it accumulates on the upstream side of the membrane. This "polarization" retards solvent flow osmotically.

Description

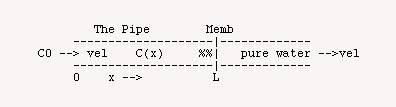
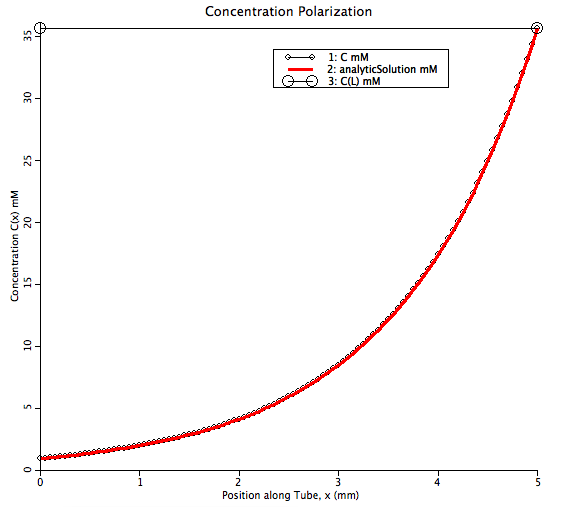
  Concentration polarization: From a solution of constant concentration C0 there 
  is flow of the solution through a tube towards a filtering membrane at 
  distance L from the inlet. The tube diameter doesn't matter and we consider 
  only fluid velocity toward the membrane and diffusion of solute, both being 
  one-dimensional normal to the membrane surface. The solute does NOT permeate, 
  and therefore become concentrated above the membrane, creating a gradient
  in concentration, dCdx or C:x. The solute activity coefficient
  is assumed to remain constant at 1. The buildup in C(x) will retard
  solvent flow osmotically.unless pressure is raised to maintain flow.	

Equations

The basic equation for this problem in the steady state balances the diffusion at any point upstream of the membrane with the convection of the solute downstream towards the membrane.

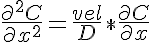
where C is the concentration of the diffusing species, D is the rate of diffusion of the species in the axial direction and vel is the velocity of the solute/solvent mix entering the tube. Two boundary conditions are applied at the tube entrance:

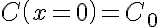
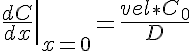
where C₀ is the concentration of the solute at the entrance to the tube. The analytical solution to this problem is given by:

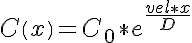
The equations for this model may be viewed by running the JSim model applet and clicking on the Source tab at the bottom left of JSim's Run Time graphical user interface. The equations are written in JSim's Mathematical Modeling Language (MML). See the Introduction to MML and the MML Reference Manual. Additional documentation for MML can be found by using the search option at the Physiome home page.