This cooperativity binding model exhibits bistable bifurcation.

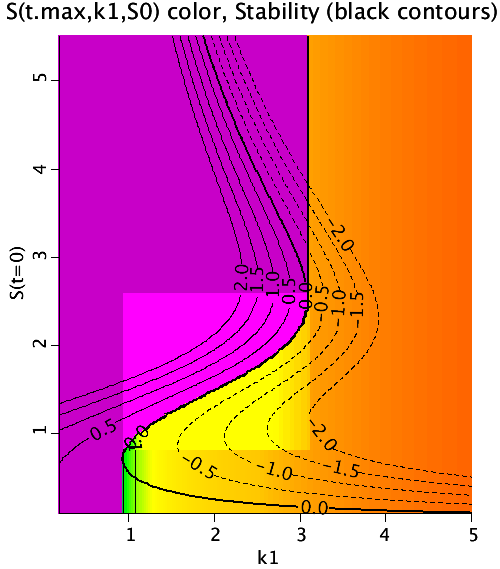
Figure 1: Cooperativity equation with bistable bifurcation.

Description

This is a model of binding cooperativity which is bistable.
The differential equation for S is a function of
X0, Vmax, n, and k1, and t, with initial value S0.

The goal is to explore the stability as a function of
k1 and S0, for fixed values of X0, Vmax, and n.

The realDomain values are defined for t (time) k1 and S0 
(the initial value of S). The final value of S (S(t.max,k1,S0) 
is contoured in color. Notice the sharp demarcation between the
purple region and orange region where a small shift in k1 and S0
give very different final values. 

The plot also shows the stability line (where the
ODE does not change value (dark contour labelled 0.)
However between approximately 0.75 < S < 2.5
the smallest displacements from the stability line
yields very different steady state answers. This
piece of the stability line is a bifurcation.  Along 
the rest of the dS/dt=0 curve, small perturbations in k1 
and S0 cause only small perturbations in the steady state
solutions.

The line where dS/dt=0 is given as

      X0+Vmax*S^n/(15+S^n) - k1*S = 0.

Setting k1 =2, X0 = 1/2, Vmax = 10, and n=4, we have a 
quintic equation. Solving for S, there are 3 real roots and
two complex roots. The real roots occur at
S= 0.251329652519894, 1.49225862823290, 5.14522788409661.

The unstable point is at S=1.4922586282329 and this is shown
by loading the BistabilityLOOPS parameter set, running LOOPS,
and inspecting the Bistability plot page. S0 = 1.491 and 1.492 
have a steady state value = 0.2513965, whereas S0 = 1.493 and
1.494 have a steady state value of 5.1452279. These two different
final values are the other two real roots when solving dS/dt=0.

Equations

     Cooperativity equation

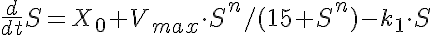
The equations for this model may be viewed by running the JSim model applet and clicking on the Source tab at the bottom left of JSim's Run Time graphical user interface. The equations are written in JSim's Mathematical Modeling Language (MML). See the Introduction to MML and the MML Reference Manual. Additional documentation for MML can be found by using the search option at the Physiome home page.