Compute the crosscovariance for the output of two similar first order operators whose input is the same random variable.

Description

A random variable (Gaussianly distributed random numbers
with mean = 0 and variance = 1), RanVar, is filtered by 
two different first order operators of the form

	tau1*d(input1)/dt = RanVar-input1 and
        tau2*d(input2)/dt = RanVar-input2.

The crosscovariance at a given lag is calculated

                               n
                             -----
                              \    input1(i)
                     Mean1 =   )   ---------
                              /     n
                             -----
                             i = 1

                               n
                             -----
                              \    input2(i)
                     Mean2 =   )   ---------
                              /     n
                             -----
                             i = 1


                            n - lag
                             -----
                              \
                               )    (input1(i) - Mean1) (input2(i + lag) - Mean2)
                              /
                             -----
                             i = 1
  crosscovariance(lag) = ------------------------------------------------
                                            n-1

The crosscovariance at zero lag  is the estimated covariance. The crosscorrelation
is the crosscovariance normalized by the product of the standard deviations
of each series..

                            crosscovariance(lag)
  crossocorrelation(lag) = ---------------------
                               stdev1*stdev2

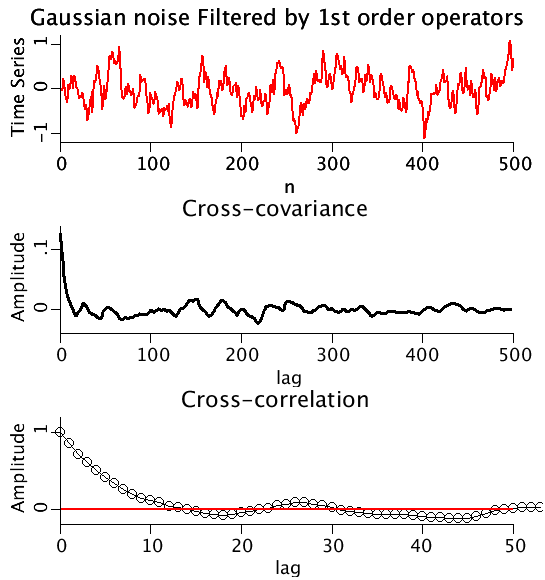
Upper Panel: The ouput of a 1st order operator with random Gaussian input.
Middle Panel: The cross-covariance as a function of lag.
Lower Panel: The cross-correlation (cross-covariance normalized by the product of the standard deviations).

Equations

None.

The equations for this model may be viewed by running the JSim model applet and clicking on the Source tab at the bottom left of JSim's Run Time graphical user interface. The equations are written in JSim's Mathematical Modeling Language (MML). See the Introduction to MML and the MML Reference Manual. Additional documentation for MML can be found by using the search option at the Physiome home page.