Axially distributed 2-region capillary-tissue exchange operator for Albumin binding fatty acid at a particular binding site.

Description

 One-dimensional convection-permeataion-diffusion-
 reaction model consisting of two concentric cylinders separated by a 
 membrane. The central plasma region of volume Vp has flow Fp, first order 
 consumption, Gp, and axial diffusion (disperion) Dp. Units are physiological
 per gram of tissue so that a single unit can model a homogeneously perfused 
 organ. Radial diffusion is assumed instantaneous (short radial distances).
 Exchange into a second surrounding non-flowing region is passive with
 conductance, PS, the Permeability capillary Surface area product. 
 The interstitial fluid region, isf, of volume Visf, like the capillary, 
 is axially distributed, and the axial gradients are dissipated by
 concentration-independent axial diffusion or dispersion, D cm^2/s. Radial diffusion 
 within this space is considered instantaneous, and consumption, Gisf, is
 first order. This model is used in multicapillary models as one of a set of 
 units in parallel.   

Transcap extraction of F when there is only one, not multiple, independent binding sites on albumin.
1. Albumin flow is the driving event. Assume const flow. All sites move downstream together, same velocity.
   Piston flow.
2. Loss across endothelium has same params for all sites since the free F pool doesn't distinguish sites.
3. Assume equilibration BEFORE entry into capillary, i.e. the site occupancy is known from the I.C's
4. On-off equations for each site, exchanging with free F, will account for redistribution using the plasma 
   concentration of F. (A shell of F in the immediate locale of Alb is NOT considered here.) Use the Independent 
   Sites Model, not the Sequential Binding Model.
5. Capillary permeability is axially uniform, passive.
6. No return flux from tissue = Visf in region 2 is infinite. 
7. Therefore need: 1 free alb, 1 free F,  N binding sites with x-dependent occupancy.
   Minimum for 1-site: solute A, AF, and F, with only F permeating,i.e. Inputs for Cp, C1p, C1pF, FF simultaneous
8. Wish to determine the dependency of the transmembrane flux on concn. The expectation
   is that at High F, the off-rates of thelowest affinity sites will contribute most, and give 
   the highest fluxes, but lowest F fluxes per unit free F, and lowest extraction fraction. 
   Define extraction as the fraction of total F removed in single transcap passage.
9. Compare with 1983 data (Vusse etal.) re decrement in Extraction vs F with constant Atot/Ftot.

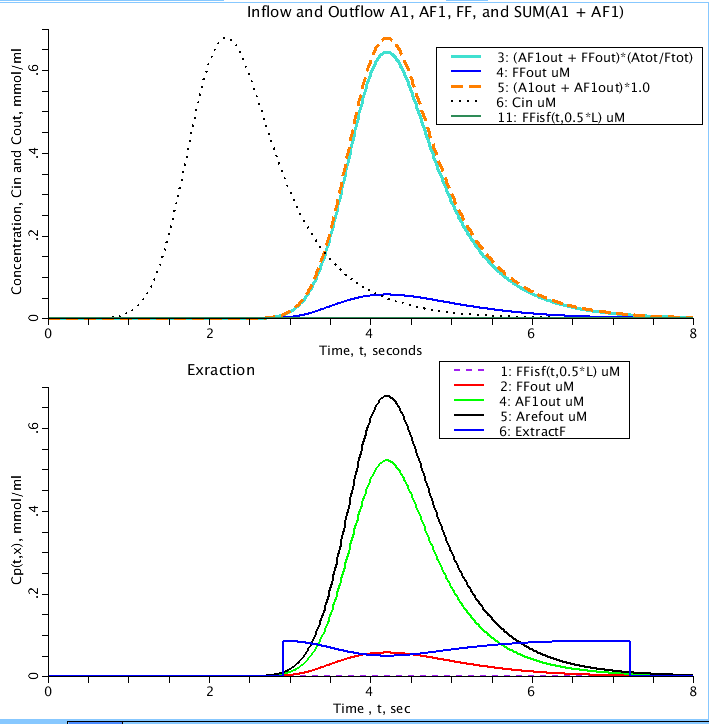
Figure: (Top) Inflow (Cin) and outflow of solutes through a capillary with exchange into the ISF of free fatty-acid (FF) and binding of FF to albumin (A). A1out is the conentration of albumin with site one free leaving the capillary. AF1out is the concentration of albumin with site one ocupied by FF leaving the capillary. FFisf is the concentration of FF in isf region at a point in the isf halfway down the capillary of length L. FFout is the concentration of FF leaving the capillary.Atot and Ftot are the total concentration of albumin and FF in teh system. Bottom Amount of free fatty-acid extracted (ExtractF) versus outflows as a function of time. Arefout is the reference albumin (Does not bind with FF) concentration leaving the capillary.

Equations

The equations for this model may be viewed by running the JSim model applet and clicking on the Source tab at the bottom left of JSim's Run Time graphical user interface. The equations are written in JSim's Mathematical Modeling Language (MML). See the Introduction to MML and the MML Reference Manual. Additional documentation for MML can be found by using the search option at the Physiome home page.