Models Forced Expiratory Volume procedure using the linear one chamber compartment model taken from Bates (ch. 3)

Description

	This model adapts the single compartment lung as developed by Bates to the 
forced expiratory volume (FEV) procedure. The model includes a resistance term 
(represented by airway resistance) and a spring recoil term (spring resistance 
represented by 1 / lung compliance, 1/C) for the lung. Several commonly used lung 
volumes have been calculated and reported. This model can be modified to add to a 
larger model or can be used alone as a simple model. A data set has been added and 
a fit has been attempted.
	This model has several problems. First, it cannot be fit to a real data 
curve, thus invalidating the model for real world use. A more accurate model has been
created using the Maxwell viscoelastic system as also developed by Bates (insert 
model number, Bates pg 117-118). The viscoelastic behavior contributed by the 
addition of the Maxwell body gives the more accurate model a 2-component outflow and 
the ability to fit to actual data. However, the following problems are shared by both 
models.
	The second problem is that the driving pressure of the system is external, 
not from the chest wall, and therefore acts like a respirator pumping up the lung 
with positive pressure and sucking the air out with negative pressure, the reverse of
normal ventilation. This is the opposite of the "forced expiration" compressing the 
chest and raising intrapleural pressure. 
	The third problem is that the compliance, C1, is constant instead of being 
functions of the volume. In reality the FEV ends, at Vlung = Functional Reserve 
Capacity - Expiratory Reserve Volume = Residual Volume, when the force of chest 
muscle contraction cannot make the chest smaller (equivalent to compressing the 
spring further). The passive pressure-volumes curves should be concave upward for 
both chest and lungs at volumes above FRC, At FRC the chest recoil is toward 
enlargment and the lung recoil is toward shrinkage, so the combination produces a 
negative intrapleural pressure at rest.
	Fourth, air is assumed to be incompressible. In reality air flow inward 
through the mouth is less than flow into the lungs because of the additional volume 
contributed by water vapor pressure rising to 47 mmHg. With an FEV the volume is 
compressed, often by 1/8th, i.e. 100 mmHg exhalation pressure added to 760 mmHg.

Figure

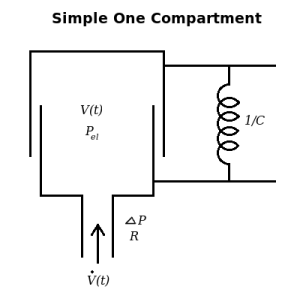
Equations

The equations for this model may be viewed by running the JSim model applet and clicking on the Source tab at the bottom left of JSim's Run Time graphical user interface. The equations are written in JSim's Mathematical Modeling Language (MML). See the Introduction to MML and the MML Reference Manual. Additional documentation for MML can be found by using the search option at the Physiome home page.