The autoregulatory device (ARD) developed by Gao et al. is reproduced here to simulate the autoregulation of cerebral blood flow in the 300 to 50 micron diameter vessels.

Description

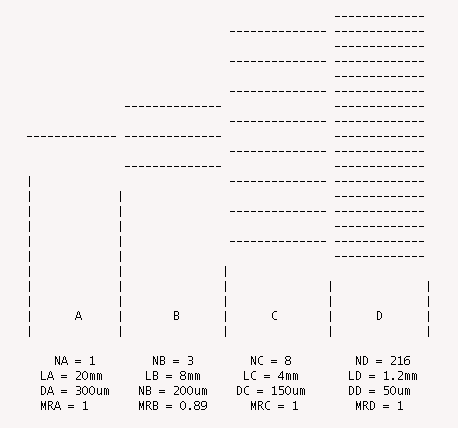
  This model represents the autoregulation of blood flow through a portion 
  of the cerebral microvasculature as developed by Gao et al. (Am J Physiol
  274:H1023-H1031, 1998).  The microvasculature is described by a 
  representative segment model where each of the four vascular regions are 
  described by a specified number of identical vessel segments.  In the first
  region with a control diameter of 300 microns there is a single segment.  
  In the second region with a control diameter of 200 microns there are 3
  segments.  The third region with a control diameter of 150 microns has 8
  segments while the final region with a control diameter of 50 microns has
  216 segments.  

  The number of segments in each region is determined in such a manner that 
  Ni*Di^3 is relatively constant throughout the network.  This is based 
  on Murray's cost analysis of network branching morphology (PNAS 12:207-214,
  1926). The vessel segments in each region are then allowed to vary as a 
  function of the  systemic mean arterial pressure (MAP) according to 
  empirical fits to the in vivo data of Kontos et al. (Am J Physiol 234:
  H371-H383, 1978). 

  It should be noted that the empirical expression used to fit the Kontos et
  al. data, Equation 3, is incorrect in the published paper. See Equations 
  section below. 

  The parameters from Table 3 in the paper reproduce the diameter versus
  pressure curves shown in Figure 5 with the equation quoted below. 
 

where MR is the Murray's law ratio: Nx*Rx^3 / NA*RA^3.

Equations

The autoregulatory device developed by Gao uses an empirical fit to data from Kontos et al. where the equation for the variation in diameter d_i as a function of the systemic

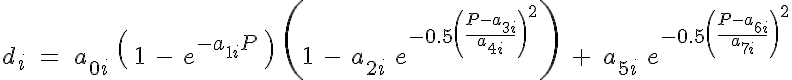
where each compartment, i, of the autoregulatory device (i = A through D) has a different regulatory response based on the set of fit parameters, a_0i to a_7i . The resistances in each compartment can then be calculated from the diameter of the segments using the following expression:

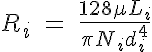
where R_i is the resistance in compartment i, 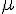 is the viscosity of blood, L_i is the segment length in compartment i, N_i is the number of segments in compartment i and d_i is the segment diameter determined from the empirical fit above.

The resistances in each compartment are then added to get the total resistance of the ARD and then the flowrate, Q, and effective diameter, d_eff, can then be calculated from the following expressions:

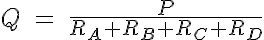
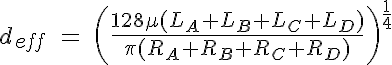
The equations for this model may be viewed by running the JSim model applet and clicking on the Source tab at the bottom left of JSim's Run Time graphical user interface. The equations are written in JSim's Mathematical Modeling Language (MML). See the Introduction to MML and the MML Reference Manual. Additional documentation for MML can be found by using the search option at the Physiome home page.