Model of transmembrane resting potential due to concentration differences in K, Na, and Ca across a membrane with constant conductance for each ion.
Description
Calculation of steady-state resting potential, EGoldman, due to three ion-selective channel conductances but no Na Pump. Allows changing of concentrations and temperature in order to explore the Nernst and Goldman potential relationships. Display is set up using log scaling on bottom two panels. Set rateo to a negative rate such as -1 mv/ms to show that Em and Egoldman changes as Ki decreases. Model accounts for two monovalent cations, K and Na, and one divalent ion, Ca, all driven by their electrochem gradients. Membrane separates 2 regions of fixed concentrations, Iono and Ioni. Solute activities are unity. Currents reach S.S. instantaneously. Nernst potentials are independent of conductance. Given a single channel conductance about 300 pSiemens; 10^6 chan -> 300 uS. What would be the the current flow at the starting concentrations Ko=5 and Ki=150 mM? Insert suitable concentrations for Ca, e.g. 1e-4 and 2 mM, and for Na, 12 and 144 mM and determine the slopes. See Notes within this .proj file for guidance.
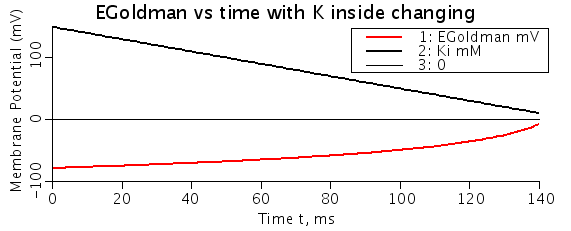
Figure: EGoldman resting potential dependence on ion concentration (Ki). Ki decreases at a constant rate. The EGoldman potential converges to zero as Ki nears zero (Init conc of 150 mM). Note: Ki plot is concentration (mM).
Equations
The equations for this model may be viewed by running the JSim model applet and clicking on the Source tab at the bottom left of JSim's Run Time graphical user interface. The equations are written in JSim's Mathematical Modeling Language (MML). See the Introduction to MML and the MML Reference Manual. Additional documentation for MML can be found by using the search option at the Physiome home page.
- Download JSim model MML code (text):
- Download translated SBML version of model (if available):
We welcome comments and feedback for this model. Please use the button below to send comments:
Goldman David E. Potential, impedance, and rectification in membranes. J Gen Physiol 27: 37-60, 1943. Sperelakis N. Origin of the cardiac resting potential. Appendix: Physical principles, derivations, and applications. In: Handbook of Physiology, Sec. 2, The Cardiovascular System. Vol. 1, edited by Berne RM, Sperelakis N, and Geiger SR. Baltimore: Waverly Press, Inc., 1979, pp 187-267. Hille B. Ion Channels of Excitable Membranes, Third Edition. Sunderland, Massachusetts: Sinauer Associates, 2001, 814 pp. page 19, Figure 1.6
Please cite https://www.imagwiki.nibib.nih.gov/physiome in any publication for which this software is used and send one reprint to the address given below:
The National Simulation Resource, Director J. B. Bassingthwaighte, Department of Bioengineering, University of Washington, Seattle WA 98195-5061.
Model development and archiving support at https://www.imagwiki.nibib.nih.gov/physiome provided by the following grants: NIH U01HL122199 Analyzing the Cardiac Power Grid, 09/15/2015 - 05/31/2020, NIH/NIBIB BE08407 Software Integration, JSim and SBW 6/1/09-5/31/13; NIH/NHLBI T15 HL88516-01 Modeling for Heart, Lung and Blood: From Cell to Organ, 4/1/07-3/31/11; NSF BES-0506477 Adaptive Multi-Scale Model Simulation, 8/15/05-7/31/08; NIH/NHLBI R01 HL073598 Core 3: 3D Imaging and Computer Modeling of the Respiratory Tract, 9/1/04-8/31/09; as well as prior support from NIH/NCRR P41 RR01243 Simulation Resource in Circulatory Mass Transport and Exchange, 12/1/1980-11/30/01 and NIH/NIBIB R01 EB001973 JSim: A Simulation Analysis Platform, 3/1/02-2/28/07.

