Oxygen and O-15 tracer content of Blood at 37C (time-dependent/transient oxygen flow), Hill model. import nsrunit; unit conversion on;
Description
This model shows the summation of Hb-bound and dissolved oxygen in blood as a transiet process. Where the original model used the Hill equation to generate saturation curves as a function of the partial pressure of O2, this model shows the effect on saturation as the oxygen levels in the blood increase and decrease. Furthermore, in this model the effect of an O-15 tracer competing with the O-16 to oxygenate the hemoglobin is considered. The saturation curves are evidence of how increased competition leads to faster saturation. The amount of 0-15 can be varied O15 is a molecule of with radioactive oxygen in the place of the non-radioactive isotope used in PET imaging to measure blood flow. Hematocrit can be varied. The water content of plasma and RBC are average values and will differ from states of over or underhydration, or hypo- or hyper-proteinemia. Other models may be subsituted for the Hill model for HbO saturations. The conditions assumed here are pH 7.4, pCO2 40 mmHg, Temperature 37C, 2,3 DPG at 4.35 mM.
Equations
None.
The equations for this model may be viewed by running the JSim model applet and clicking on the Source tab at the bottom left of JSim's Run Time graphical user interface. The equations are written in JSim's Mathematical Modeling Language (MML). See the Introduction to MML and the MML Reference Manual. Additional documentation for MML can be found by using the search option at the Physiome home page.
Example equations, remove as needed: 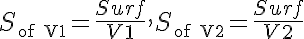
- Download JSim model MML code (text):
- Download translated SBML version of model (if available):
We welcome comments and feedback for this model. Please use the button below to send comments:
Adair GS. The hemoglobin system. VI. The oxygen dissociation curve of hemoglobin. J Biol Chem 63: 529-545, 1925. Dash RK and Bassingthwaighte JB. Blood HbO2 and HbCO2 dissociation curves at varied O2, CO2, pH, 2,3-DPG and temperature levels. Ann Biomed Eng 32(12): 1676-1693, 2004. Dash RK and Bassingthwaighte JB. Simultaneous blood-tissue exchange of oxygen, carbon dioxide, bicarbonate and hydrogen ion. Ann Biomed Eng 34(7): 1129-1148. 2006. Hill AV. The possible effects of the aggregation of the molecules of haemoglobin on its dissociation curves. J Physiol 40: iv-vii, 1910 Hill R: Oxygen dissociation curves of muscle hemoglobin. Proc Roy Soc Lond B 120: 472-480, 1936. Roughton FJW, Deland EC, Kernohan JC, and Severinghaus JW: Some recent studies of the oxyhemoglobin dissociation curve of human blood under physiological conditions and the fitting of the Adair equation to the standard curve. In: Oxygen Affinity of Hemoglobin and Red Cell Acid Base Status. Proceedings of the Alfred Benzon Symposium IV Held at the Premises of the Royal Danish Academy of Sciences and Letters, Copenhagen 17-22 May, 1971, edited by Rorth M and Astrup P. Copenhagen: Munksgaard, 1972, p. 73-81. Winslow RM, Swenberg M-L, Berger RL, Shrager RI, Luzzana M, Samaja M,and Rossi-Bernardi L: Oxygen equilibrium curve of normal human blood and its evaluation by Adair's equation. J Biol Chem 252: 2331-2337, 1977.
Please cite https://www.imagwiki.nibib.nih.gov/physiome in any publication for which this software is used and send one reprint to the address given below:
The National Simulation Resource, Director J. B. Bassingthwaighte, Department of Bioengineering, University of Washington, Seattle WA 98195-5061.
Model development and archiving support at https://www.imagwiki.nibib.nih.gov/physiome provided by the following grants: NIH U01HL122199 Analyzing the Cardiac Power Grid, 09/15/2015 - 05/31/2020, NIH/NIBIB BE08407 Software Integration, JSim and SBW 6/1/09-5/31/13; NIH/NHLBI T15 HL88516-01 Modeling for Heart, Lung and Blood: From Cell to Organ, 4/1/07-3/31/11; NSF BES-0506477 Adaptive Multi-Scale Model Simulation, 8/15/05-7/31/08; NIH/NHLBI R01 HL073598 Core 3: 3D Imaging and Computer Modeling of the Respiratory Tract, 9/1/04-8/31/09; as well as prior support from NIH/NCRR P41 RR01243 Simulation Resource in Circulatory Mass Transport and Exchange, 12/1/1980-11/30/01 and NIH/NIBIB R01 EB001973 JSim: A Simulation Analysis Platform, 3/1/02-2/28/07.

