This model represents changes of blood viscosity due to the Fahraeus-Lindqvist effect as observed by Pries, Secomb et al. for flow in the rat mesentery.

Description

 This blood viscosity model represents the in vivo viscosity relationship, developed by 
 Axel Pries, Tim Secomb et al., of the Fahraeus-Lindqvist effect. The development by 
 Pries et al. is the latest in a series of refinements of the initial observation made 
 by Fahraeus, that the hematocrit of blood flowing through a narrow tube differs from the 
 hematocrit of the blood supply at the inlet.

 Fahraeus's observation led him to distinguish between tube and discharge hematocrit and, 
 more to the point of this model, led to his conclusion, with Lindqvist, that effective 
 viscosity of the blood in narrow tubes must also vary with the diameter of the tube. Fahraeus 
 and Lindqvist noticed that in tubes greater than 1 mm in diameter the bulk viscosity values 
 for blood were acceptable for matching blood flow. On the other hand, as the tubes became 
 smaller the effective viscosity was reduced. The effective viscosity is defined here as the 
 viscosity calculated from Poiseuille's equation for a given pressure drop, tube inside 
 diameter and tube length. Quantification and mathematical description of this effect, first in 
 narrow glass tubes and later in vivo, followed.

 The work by Pries, Secomb et al., represented in this model, shows that the effect in actual 
 vessels in vivo is not as significant as the effect in narrow glass tubes, but must be 
 accounted for in order to accurately represent flow in the microvasculature.

Equations

The expression used here is for the effective viscosity of blood relative to the viscosity of plasma, and therefore the expression is unitless.

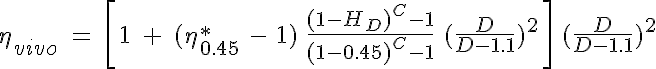
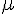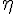where H_D is the discharge hematocrit, D is the diameter of the vessel lumen (in m), ^*_0.45 is the relative effective viscosity at 45% hematocrit and C is the shape of the dependence of the viscosity on discharge hemtocrit. The expression for 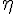^*_0.45 is given by:

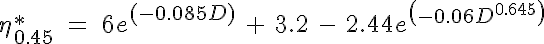
and C is given by:

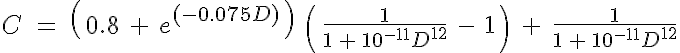
The equations for this model may be viewed by running the JSim model applet and clicking on the Source tab at the bottom left of JSim's Run Time graphical user interface. The equations are written in JSim's Mathematical Modeling Language (MML). See the Introduction to MML and the MML Reference Manual. Additional documentation for MML can be found by using the search option at the Physiome home page.