A n iterative procedure is used to draw the Logistic Map.

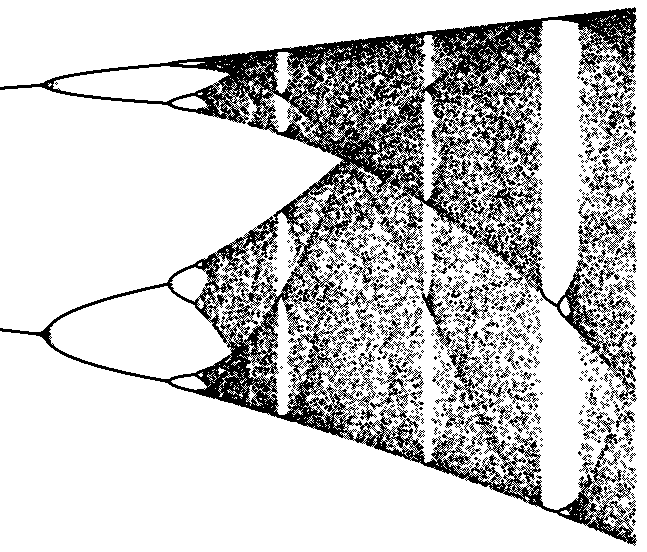
Figure 1: The logistic map.

Description

The sequence given by

  x(n+1) = r * x(n) * ( 1 - x(n) ), x(0) = random()
  0<=r<=4

where random() is a uniform random number between 0 and 1
can be used to generate the Logistic Map. The x values
after 200 iterations are plotted as a function of r to
produce the logistic map.

For r = 2.8, the process converges to a single value.
For r = 3.3, the process oscillates between two values.
For r = 3.5, the process oscillates between four values.
For r = 3.8, the process is chaotic even though it is deterministic.

Plotting pairs of points ( x(n), x(n+1) ) reveals a one
dimensional curve (parabola). The logistic map is a fractal
because if any part of it is expanded, it reveals a similar
structure.

The logistic map shows bifurcating behavior. Small changes in
r can change the set of x values from a finite number to an 
infinite number.

There are other variations of this algorithm which are 
also called the Logistic equation, e.g.

 x(n+1) = x(n) + r * x(n) * ( 1 - x(n) ), x(0) = random()
  0<=r<=3.

Equations

     Iterative equation for Logistic Map

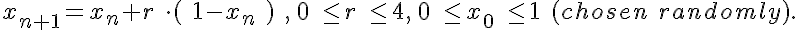
The equations for this model may be viewed by running the JSim model applet and clicking on the Source tab at the bottom left of JSim's Run Time graphical user interface. The equations are written in JSim's Mathematical Modeling Language (MML). See the Introduction to MML and the MML Reference Manual. Additional documentation for MML can be found by using the search option at the Physiome home page.