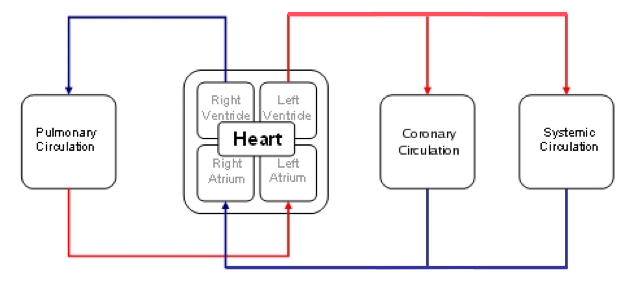
A closed loop circulatory model with varying elastance heart, pulmonary, coronary and systemic circulatory loops and actively regulating arterioles in the systemic circulation responding to pressure and shear stress on the vessel walls.
Description
This model is identical to the lumped parameter circulation model except for the insertion of an arteriolar vessel compartment which varies resistance and compliance actively based on the intraluminal pressure and vessel wall shear stress. The reason for the incorporation of a vasoactive arteriolar compartment is that much of the regulation of blood flow throughout the microvasculature can be attributed to regulatory responses in the arterioles. Two known local regulatory responses are that to changes in pressure (myogenic response) and that to changes in flow (shear-dependent response) and both are characterized here. There are other local and global responses such as conducted response, countercurrent flow response and sympathetic responses which are not characterized in this model. The ultimate goal of incorporating a regulatory response in a circulatory model is to describe the active response of the microvasculature to changes in blood volume and systemic pressure which occur in hemorrhagic injury.
Below we compare the beat to beat pressure response of the model with (top) and without (bottom) vasoactive response:
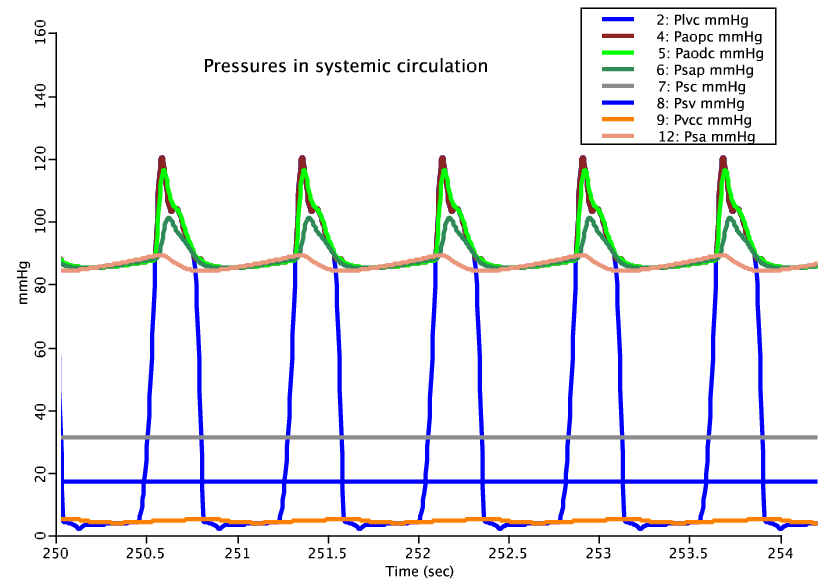
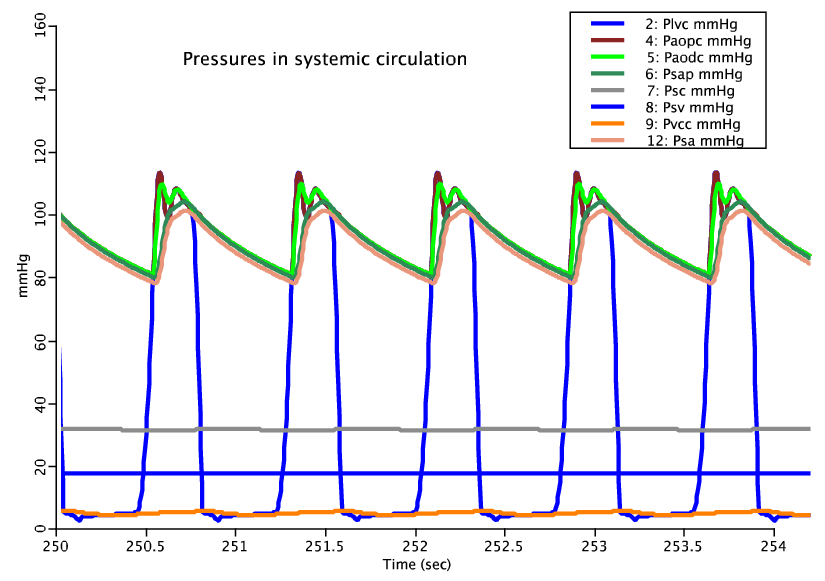
Figure: Where subcripts lvc, aopc, aodc, sap, sa, sc, sv and vcc stand for left ventricle, proximal aorta, distal aorta, systemic arteries, systemic arterioles, systemic capillaries, systemic veins and vena cava respectively. The pulse shape of the arterioles with vasoactive response is considerably damped because the vessels are instantaneously reacting to their local pressure and shear conditions. In actuality the local response can be divided into an active and passive component with two distinct time scales. The passive portion of the response has a time constant on the order of 1 second while the active vascular smooth muscle response of the vessel has a time constant on the order of 1 minute. Therefore if these two responses are separated and allowed to operate with their respective time characteristics, a more faithful representation of the beat to beat pulse pressue response will result. This model should still faithfully respond to a long time scale adjustment in systemic pressure.
Equations
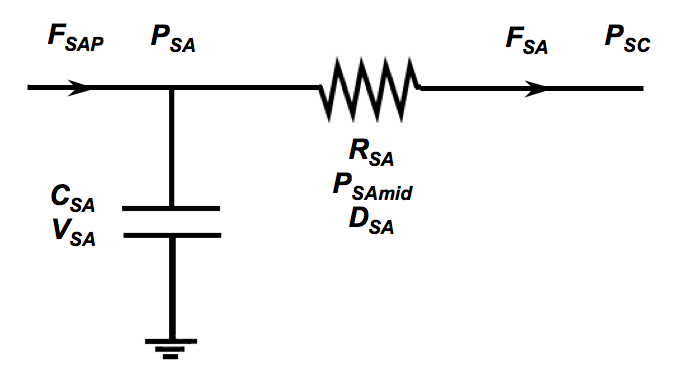
In a lumped parameter model each compartment of the systemic circulation is described by the flow analog of an RC circuit similar to what is shown below. In the figure flow is F, pressure is P, total resistance is R, individual vessel diameter is D, compliance is C and total volume is V. In the vasoactive arteriolar compartment the resistance to flow, RSA, and vessel compliance, CSA, depend upon the average compartment pressure, PSAmid = (PSA - PSC)/2, and the wall shear stress, SA. If we are given an initial blood volume and a typical resistance of all the arterioles in this compartment we are able to determine the total number of vessels in the compartment and their effective length explicitly. All the arterioles in the compartment are identical and the response to pressure and shear stress is determined from experimental data from Sun et al. (see reference below.)
A poster, presented at the Mathematical Biosciences Institute at Ohio State, describing the equations used to determine pressure, flow, total resistance to flow, individual arteriolar diameter, compliance and total arteriolar volume in the arteriolar compartment can be downloaded here.
The equations for this model may be viewed by running the JSim model applet and clicking on the Source tab at the bottom left of JSim's Run Time graphical user interface. The equations are written in JSim's Mathematical Modeling Language (MML). See the Introduction to MML and the MML Reference Manual. Additional documentation for MML can be found by using the search option at the Physiome home page.
- Download JSim model MML code (text):
- Download translated SBML version of model (if available):
We welcome comments and feedback for this model. Please use the button below to send comments:
Brandenburg, Robert O. Cardiology: fundamentals and practice. Yearbook medical publishers, 1987. p. 49. Chung DC, Niranjan SC, Clark Jr. JW, Bidani A, Johnston WE, Zwischenberger JB, Traber DL. A dynamic model of ventricular interaction and pericardial influence. Am J Phsiol Heart Circ Physiol. 272: H2942-H2962, 1997. Golden JF, Clark JW, Stevens PM. Mathematical Modeling of Pulmonary Airway Dynamics. IEEE Transactions on Biomedical Engineering. 20(6): 397-404, 1973. Heldt T, Shim EB, Kamm RD, Mark RG. Computational modeling of cardiovascular response to orthostatic stress. Journal of Applied Physiology. 92: 1239-1254, 2002. Lu K, Clark JW, Ghorbel FH, Ware DL, Bidani A. A human cardiopulmonary system model applied to the analysis of the Valsalva maneuver. Am J Physiol Heart Circ Physiol. 281: H2661-H2679, 2001. Rideout VC. Mathematical computer modeling of physiological systems. Englewood Cliffs, NJ: Prentice Hall, 1991, 261 pp. Sun Y, Beshara M, Lucariello RJ, Chiaramida SA. A comprehensive model for right-left heart interaction under the influence of pericardium and baroreflex. Am J Physiol Heart Circ Physiol. 272: H1499-H1515, 1997. Zinemanas D, Beyar R, Sideman S. Relating mechanics, blood flow and mass transport in the cardiac muscle. Int. J. Heat Mass Transfer. 37(suppl. 1) 191-205, 1994.
Please cite https://www.imagwiki.nibib.nih.gov/physiome in any publication for which this software is used and send one reprint to the address given below:
The National Simulation Resource, Director J. B. Bassingthwaighte, Department of Bioengineering, University of Washington, Seattle WA 98195-5061.
Model development and archiving support at https://www.imagwiki.nibib.nih.gov/physiome provided by the following grants: NIH U01HL122199 Analyzing the Cardiac Power Grid, 09/15/2015 - 05/31/2020, NIH/NIBIB BE08407 Software Integration, JSim and SBW 6/1/09-5/31/13; NIH/NHLBI T15 HL88516-01 Modeling for Heart, Lung and Blood: From Cell to Organ, 4/1/07-3/31/11; NSF BES-0506477 Adaptive Multi-Scale Model Simulation, 8/15/05-7/31/08; NIH/NHLBI R01 HL073598 Core 3: 3D Imaging and Computer Modeling of the Respiratory Tract, 9/1/04-8/31/09; as well as prior support from NIH/NCRR P41 RR01243 Simulation Resource in Circulatory Mass Transport and Exchange, 12/1/1980-11/30/01 and NIH/NIBIB R01 EB001973 JSim: A Simulation Analysis Platform, 3/1/02-2/28/07.

