2-region capillary-tissue exch of iodinated contrast in solid tumor.
Description
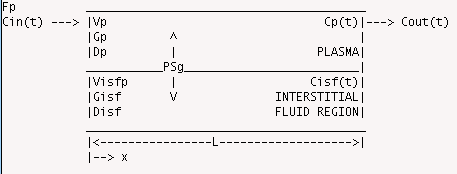
One-dimensional convection-permeation-diffusion- reaction model consisting of two concentric cylinders separated by a membrane. The central plasma region of volume Vp has flow Fp, no consumption, but has axial diffusion (disperion) Dp. Units are physiological per gram of tissue so that a single unit can model a homogeeously perfused region. Radial diffusion is assumed instantaneous (short radial distances). Exchange into a second surrounding non-flowing region is passive bidirectional with conductance, PS, the Permeability capillary Surface area product. The interstitial fluid region, isf, of volume Visfp (see Notes) is axially distributed, and the gradients axially are dissipated by a concentration-independent axial diffusion or dispersion. Radial diffusion within this space is considered instantaneous, and there is no consumption. This model is sutiable for use in multicapillary models as one of a set of units in parallel.
Equations
The equations for this model may be viewed by running the JSim model applet and clicking on the Source tab at the bottom left of JSim's Run Time graphical user interface. The equations are written in JSim's Mathematical Modeling Language (MML). See the Introduction to MML and the MML Reference Manual. Additional documentation for MML can be found by using the search option at the Physiome home page.
- Download JSim model MML code (text):
- Download translated SBML version of model (if available):
- No SBML translation currently available.
- Information on SBML conversion in JSim
We welcome comments and feedback for this model. Please use the button below to send comments:
Sangren WC and Sheppard CW.; A mathematical derivation of the exchange of a labeled substance between a liquid flowing in a vessel and an external compartment. Bull Math Biophys 15: 387-394, 1953 (This gives an analytic solution for the two-region model.) Goresky CA, Ziegler WH, and Bach GG.; Capillary exchange modeling: Barrier-limited and flow-limited distribution. Circ Res 27: 739-764, 1970. (This gives another derivation of the analytical form, and uses the model in both single and multicapillary models. Bassingthwaighte JB.; A concurrent flow model for extraction during transcapillary passage. Circ Res 35: 483-503, 1974. (This gives numerical solutions, which are faster than the analytic solutions, and imbeds the model in an organ with tissue volums conserved, and with arteries and veins.) Guller B, Yipintsoi T, Orvis AL, and Bassingthwaighte JB.; Myocardial sodium extraction at varied coronary flows in the dog: Estimation of capillary permeability by residue and outflow detection. Circ Res 37: 359-378, 1975. (Application to sodium exchange in the heart.)
Please cite https://www.imagwiki.nibib.nih.gov/physiome in any publication for which this software is used and send one reprint to the address given below:
The National Simulation Resource, Director J. B. Bassingthwaighte, Department of Bioengineering, University of Washington, Seattle WA 98195-5061.
Model development and archiving support at https://www.imagwiki.nibib.nih.gov/physiome provided by the following grants: NIH U01HL122199 Analyzing the Cardiac Power Grid, 09/15/2015 - 05/31/2020, NIH/NIBIB BE08407 Software Integration, JSim and SBW 6/1/09-5/31/13; NIH/NHLBI T15 HL88516-01 Modeling for Heart, Lung and Blood: From Cell to Organ, 4/1/07-3/31/11; NSF BES-0506477 Adaptive Multi-Scale Model Simulation, 8/15/05-7/31/08; NIH/NHLBI R01 HL073598 Core 3: 3D Imaging and Computer Modeling of the Respiratory Tract, 9/1/04-8/31/09; as well as prior support from NIH/NCRR P41 RR01243 Simulation Resource in Circulatory Mass Transport and Exchange, 12/1/1980-11/30/01 and NIH/NIBIB R01 EB001973 JSim: A Simulation Analysis Platform, 3/1/02-2/28/07.

