A compliant 1 compartment lung with resistance to air flow, driven by external positive pressure ventilator.

Description

The equations governing airflow in and out of a one compartment lung are
given by the following analogy to electrical circuits:

      Airway pressure is analogous to voltage.
      Air flow is analogous to current flow.
      Volume is analogous to charge.
      Resistance to air flow is analogous to electrical resistance.
      Compliance, the relationship between pressure and volume, is
        analogous to capacitance, the relationship between charge 
        and voltage.

The model shows that various quantities are governed by exponential decay 
with time constant tau=R*Com. 
 
The main assumption is that the human lungs can be approximated as a single 
compartment modeled by an RC circuit where the quantities of interest, air 
flow, volume of air, pressure, compliance, and resistance are analogous to 
current, charge, voltage, capacitance, and resistance respectively.

GENERAL RESULTS: The ventilator, using a driving pressure of 10 mmHg gives 
an approximately normal tidal volume of 500 ml. Normally of course, the force
is provided by expansion of the chest, creating a negative pressure in the 
intrapleural space, just the oppposite of this positive pressure ventilator.

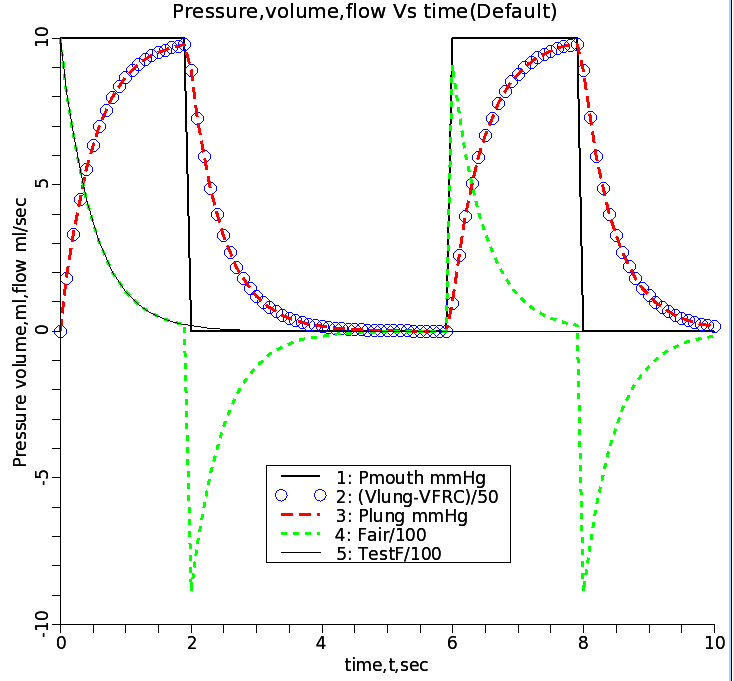
Figure: Pressure, volume, flow vs. time. The forcing ventilator pressure is Pmouth (black). 
The numerical solutions:Fair Flow at mouth (green dashes), Volume circles; Plung red dashes. 
TestF is black line (exp(-t/Res*com)), a verification test fitting Fair(t).

Equations

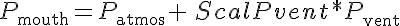
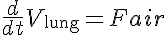
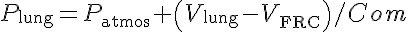
where P_mouth is the pressure at the mouth; P _atmos, Ref pressure, external to body; P_vent, the driving pressure from a ventilator; ScalPvent, scaler of amplitude of Pvent; P_lung is the pressure in the lung; Fair is the air flow at the mouth; R is the resistance of the airway; Com is the compliance of the lung; V_FRC is the functional residual capacity of the lung; and V_lung is the volume of air in the lung.

The equations for this model may be viewed by running the JSim model applet and clicking on the Source tab at the bottom left of JSim's Run Time graphical user interface. The equations are written in JSim's Mathematical Modeling Language (MML). See the Introduction to MML and the MML Reference Manual. Additional documentation for MML can be found by using the search option at the Physiome home page.