One Enzyme 2 Substrates, A and B, to 2 Products, C and D, Reversible Second-order enzyme kinetic model with capacitance and reversible enzymatic reaction with binding and release kinetics for two substrates givng two products, thermodynamically constrained.

Description

   This model represents the enzymatic conversion of two substrate, A and B, to two products, C and D. 
   First is the binding of one substrate to the enzyme, E, to form EA or EB, a 1-substrate-enzyme complex, ES. 
   This binding is followed by binding the other substrate to form EAB. This is random bi-bi, not ordered.
   Next is a reaction-release event, which yields one product, C or D, and an enzyme still bound to the 
   other product. The second release yields the free enzyme and the second product.
  Note 1. The equilibrium between EAB and E is independent of the route taken: the alp1 and alp2 factors
   are to assure this. Because there is no disinction between EAB and ECD in this model alp2 = alp1 in order to
   keep the same ratio EAB/E = ECD/E.
  Note 2. The model parameters can be adjusted to fit Michaelis-Menten conditions (Substrate 
   concentrations high compared to enzyme; on/off reaction fast compared to forward 
   reaction rate) and Briggs-Haldane conditions where the On-rate is low. Reducing the [Enzyme] relative 
   to the substrate and product concnetrations reduces the effect of the capacitance of the enzyme-bound 
   forms on the kinetics of the reactions. This results in faster attainment of the steady state.  
  Note 3: Consuming the products to reduce the back flux drains the system; Segel puts all products to zero
   in order to calculat the M-M equivalent equations.
   When without a drain, the system --> equilibrium, as in this version. EquilA is the theoretical value.
  Note 4. Substrate is preserved: Stot: Sum at beginning = Sum at end.
   Enzyme is conserved: Etest.
  Note 5. This code converts the model from Random Bi-Bi to Ordered Bi Bi
   simply by putting an intital binding, k1 or j1 to zero, and likewise
   putting K_4 or j_4 to zero.
  Note 6. Segel's approach is instantaneous steady state, i.e. the binding and release 
   rates are exceeding fast, so his reaction velocities, shown by v and by v/Vmax,
   are reached instantaneously even as concentrations change. Our approach here is to 
   account for the binding and unbinding that actaully take time, and alos to account
   for the capacitance in the enzymatic reactions by accounting for the substrates an
   products bound to the enzyme. This is most important with high enyme concentrations
   or low substrate concnetrations in the range of the binding affinities. 
  Note 7. Observe that EAB achieves a peak concentration at early times when A and B
   are first sliding through the series of reaction steps starting from A and B with C 
   and D = 0. This peak is always(?) higher than at equilibrium. 


 Simultaneous substrate binding and simultaneous product release bidirectional:
        	Net reaction A + B <----> C + D    E = Enzyme concentration
          
         k1            k2              k3            k4
    A+E <-->  EA +  B <-->\         /<---->  EC + D <---> E + C
         k_1           k_2 \       /   k_3           k_4 
                            EAB=ECD
         j1            j2  /       \   j3            j4
    B+E <-->  EB + A  <-->/         \<---->  ED + C <---> E + D
         j_1           j_2            j_3            j_4       

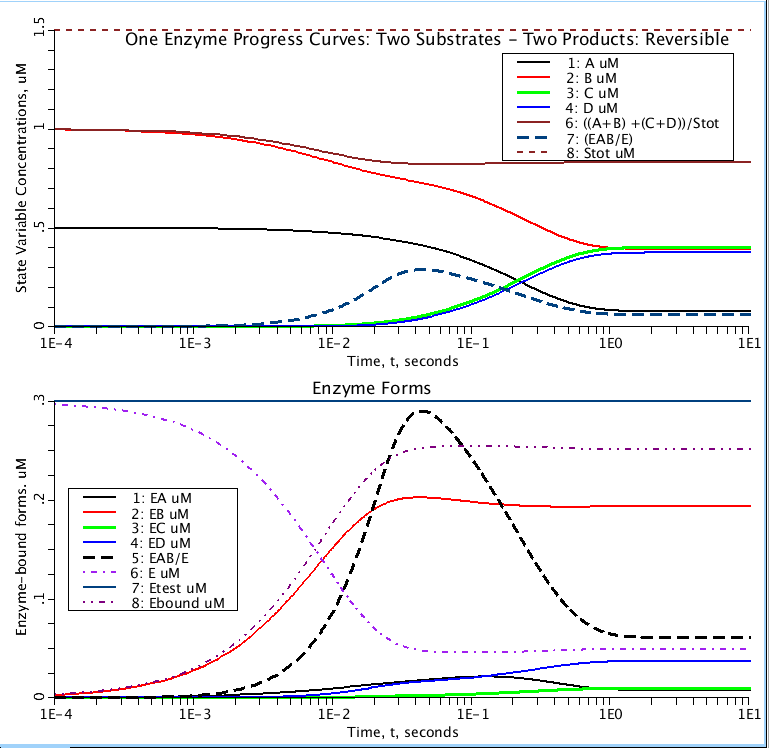
Figure: Progress curves of substrates (A,B), products (C,D), and enzyme (E). Etest is Ebound plus E (unbound). Stot is total amount of substrates and products.

Equations

The equations for this model may be viewed by running the JSim model applet and clicking on the Source tab at the bottom left of JSim's Run Time graphical user interface. The equations are written in JSim's Mathematical Modeling Language (MML). See the Introduction to MML and the MML Reference Manual. Additional documentation for MML can be found by using the search option at the Physiome home page.