Model simulates the diffusion of 11 cytosolic proteins from rabbit muscle fibers in a physiological solution. Several mechanisms which alter protein diffusion are considered including binding and hindrance to the myofilament lattice, binding to the other proteins, and protein crowding.

Description

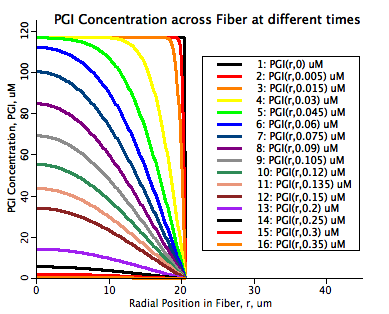
This model simulates the radial diffusion of eleven cytosolic proteins from the I-band of a rabbit skinned muscle fiber into a bathing physiological solution. Several factors reduce the diffusion of each protein from that which is expected in water. The protein diffusion is initially reduced because of the reduced diffusional path length imposed by the regular intercellular lattice structure of the myofibril. In this study this effect is called geometrical hindrance. The lattice contributes to the further reduction of protein diffusion because since it is made up of proteins provides binding opportunities to the free cytsolic proteins, here described as lattice binding. All of the proteins tracked here are known to reside in the I-band region of the muscle fiber structure so two additional effects contribute to further reduce the rate of diffusion. The first of these is the possibility of the proteins to bind together into a supramolecular complex which must dissociate into the individual proteins before they can diffuse out of the fiber. This mechanism is called complex dissociation here. The final effect accounted for here is the influence of protein crowding on protein diffusion. Regions with high protein density show a marked reduction in diffusion since each protein is responsible for obstructing the diffusion path of the other proteins. This effect was mathematically described by O'Leary (Biophys J 52:137-139, 1987.)

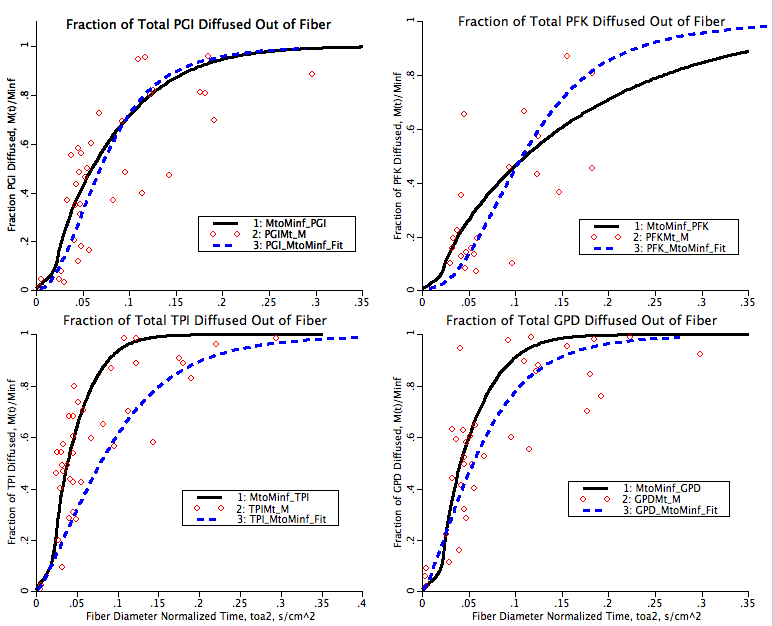
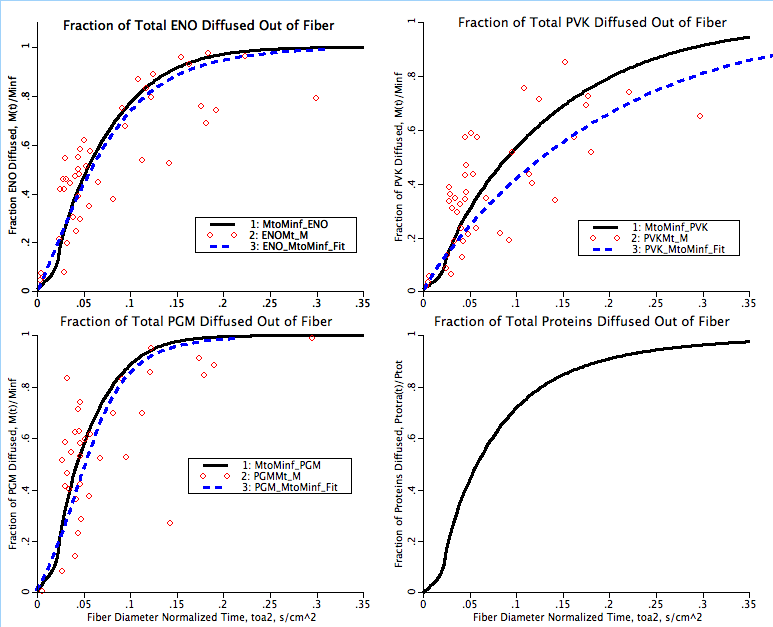
The diffusion of each of the eleven proteins is tracked simultaneously in this model and the diffusion inside the fiber is governed by the time dependent diffusion equation given in the equation section below. All four mechanisms affecting the rate of diffusion are represented in this model and the free parameters are optimized by fitting the combined model to seven sets of protein diffusion data obtained by David Maughan and Jim Vigoreaux at the University of Vermont.

To run the radial diffusion model, open up JSim and load the model project file. Select the Variable_Diff tab at the top of the JSim UI, select a plotpage to view results in the right hand pane and then hit the "Run" button at the top of the left hand pane. This simulation will take on the order of one minute to run.

There are two fits to the experimental data shown in this simulation. The first is a hand fit of four parameters used in this model, k_cd^max, P₅₀, n_cd and γ. This hand fit is followed by an optimization of the k_lb for each of the seven proteins in the I-band with data. These fits are indicated on the plotpages with the solid black line fits. The second fit is computed in a separate Matlab program where the diffusion coefficient is calculated through each data point as if it was straight radial diffusion and this varying diffusion coefficient is then fit with a power law curve fit. This curve fit tends to underestimate the rate of diffusion immediately after the initial low diffusion period indicated by the toe in the M(t)/Minf as a function of time graphs. The second fit is indicated in the plotpages as a dashed blue line.

Equations

 

The governing equation which is used in this model is that for one dimensional radial diffusion with diffusion coefficient D that varies in time only.

 

 

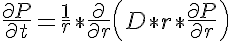
where P is the concentration of the diffusing protein, D is the rate of diffusion of the protein in the radial direction and will vary in time only, r is the radial position in the myofibril and t is time. Since D only varies with time the right hand side term can be expanded yielding:

 

 

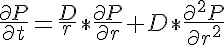
The boundary conditions for our problem are dictated by the geometry of the problem and the experimental protocol. As each myofibril is diffusing proteins into the bathing solution the myofibril is used to stir the bathing solution resulting in a protein concentration at the interface (r=a) between the myofibril and the solution of effectively zero. At the position r=0 in the myofibril no diffusional protein flux must exist. These boundary conditions are represented as:

 

 

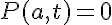
and

 

 

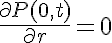
The initial condition on the protein concentration establishes the condition needed to complete the problem formulation:

 

 />

 

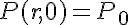where P₀ is the initial concentration of protein P.

 

Since all eleven proteins in the I-band are tracked simultaneously we have eleven coupled PDEs of the above form. They are coupled because the diffusion coefficient, D, for each protein depends on the total protein concentration in the I-band. This will be shown below but initially we must calculate the diffusion in an aquaeous solution for each protein as given by Young et al. (Biotech Bioeng 22:947-955, 1980.)

 

 

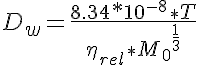
where D_w is the diffusion of the protein in water, T is the water temperature and M₀ is the molecular weight of the protein. The constant 8.34e-8 is determined in the paper by Young. Now the regular lattice structure imposed by the actin and myosin fibers arrangement reduces the diffusion coefficient through geometrical hindrance as determined by Blum et al. (Biophys J 56:995-1005, 1989.) The expression they derived is given by:

 

 

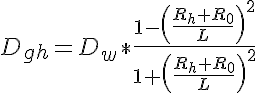
where D_gh is the diffusion coefficient reduced by geometrical hindrance, R_h is the hydraulic radius of the protein, R₀ is the radius of the actin fibers in the lattice and L is half the center to center spacing between actin fibers. The effect of proteins binding to the lattice reduces the diffusion coefficient through the following expression:

 

 

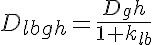
where D_lbgh is the diffusion coefficient taking into account binding to the lattice and geometrical hindrance, and k_lb is the ratio of protein bound to the lattice to that which is free in the cytosol. The last two effects couple the PDEs together since we are assuming that both the complex dissociation and protein crowding effects are functions of the total protein density in the myofibrilar I-band. The complex dissociation is structured like the lattice binding term but we further assume that at high protein density the ratio of bound to free is high and at a low protein density it reaches a minimum. So the reduction in the diffusion coefficient is given by:

 

 

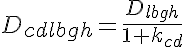
where D_cdlbgh is the diffusion coefficient taking into consideration lattice binding, geometrical hindrance and the ratio of protein bound in the supramolecular complex to that free in the cytosol, k_cd, which is given by a sigmoidal relationship of the form:

 

 

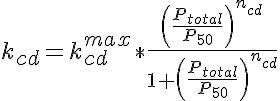
where k_cd^max is the maximal bound to free ratio, P_total is the radially averaged total protein density, P₅₀ is the protein content at the midpoint between minimal and maximal bound to free ratio and n_cd determines the steepness of transition between low to high bound to free ratio. The final effect, that of protein crowding, is given by O'Leary as:

 

 

 

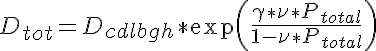
where D_tot is the diffusion coefficient accounting for all diffusion reduction mechanisms, γ is the ease of vacancy formation of the protein and ν is the protein exclusion volume. Both γ and ν are set to values typical for the average protein used in this simulation. For more complete details of the mathematical formulation please view the source code documentation in the JSim project file.

The equations for this model may be viewed by running the JSim model applet and clicking on the Source tab at the bottom left of JSim's Run Time graphical user interface. The equations are written in JSim's Mathematical Modeling Language (MML). See the Introduction to MML and the MML Reference Manual. Additional documentation for MML can be found by using the search option at the Physiome home page.

 Maughan DW, Henkin JA and Vigoreaux JO; Concentrations of glycolytic ennzymes and other cytosolic 
 proteins in the diffusible fraction of a vertebrate muscle proteome. 
 Molecular and Cellular Proteomics 4:1541-1549, 2005.

 Blum JJ, Lawler G, Reed M and Shin I; Effect of cytoskeletal geometry on intracellular diffusion.
 Biophysical Journal 56:995-1005, 1989.

 Young ME, Carroad PA and Bell RL; Estimation of diffusion coefficients of proteins
 Biotechnology and Bioengineering 22:947-955, 1980.

 O'Leary TJ; Concentration dependence of protein diffusion. Biophysical Journal 52:137-139, 1987.