This model describes the steady state regulatory vessel response to changes in pressure across and shear stress on the vessel wall.

Description

This model describes the steady state response of a regulatory vessel to combinations of changes in transmural pressure and luminal shear stress on the wall. The decreases in vessel diameter in repsonse to increases in pressure is called the 'myogenic response'. Responses to changes in shear stress is called the shear-dependent response. These two responses are local regulatory responses and have been characterized in several experimental studies. Other regulatory responses not included in this model are the metabolic, neuronal and Illustrative Diagram hormonal responses. Regulatory vessels are composed of an inner endothelial layer surrounded by circumferentially oriented vascular smooth muscle (VSM) cells and sheathed with a collagen sleeve. The VSM actively responds to both the pressure difference across the vessel wall and the shear stress on the internal surface of the vessel. The other components of the vessel wall act as a passive non-linear spring in parallel with the active VSM component. The basic model is described below and in more detail in the corresponding paper by Carlson BE and Secomb TW Microcirculation 12:327-338, 2005.

Equations

The tension in the vessel wall can be described as the tension in the passive elements of the the vessel wall added to the active VSM tension. These two components must balance the circumferential tension generated by the pressure difference across the vessel wall. So:

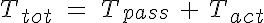
where T_tot is the pressure generated circumferential tension governed by the Law of Laplace:

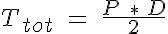
where P is the intraluminal pressure and D is the vessel diameter. The passive tension is nonlinear with respect to D and has been approximated here with an exponential:

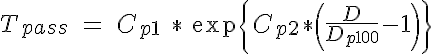
where C_p1 is the passive tension at an intraluminal pressure of 100 mmHg, C_p2 describes the steepness of the exponential and Dp100 is the diameter of the vessel in a passive state at 100 mmHg. The active tension can be further broken down into two components: A, the degree of activation of the VSM (range from 0 to 1) and T_act^max, the active tension generated by the VSM in a maximally activated state. The shape of the maximally active VSM tension curve as a function of diameter based on experimental findings has been found to be Gaussian in form and is given here by:

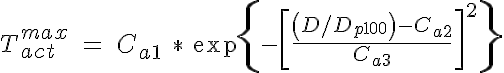
where C_a1 is the peak active tension, C_a2 is the diameter of the peak active tension normalized by the passive vessel diameter at 100 mmHg, and C_a3 is the width of the Gaussian normalized by D_p100. The VSM activation is approximated by a sigmoidal function and is given by:

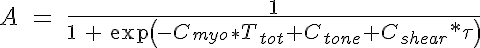
where C_myo and C_shear determine the sensitivity of the VSM activation to circumferential tension and wall shear stress respectively and C_tone is the base level of tone that is in a vessel without these stimuli. The variable 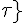  is the shear stress on the vessel wall. It must be noted that an increase in pressure, increases circumferential tension and then results in an increase in VSM activation and constriction of the vessel. An increase in shear has the opposite response. So now the circumferential tension in the vessel wall, T_tot, can be given by:

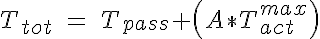
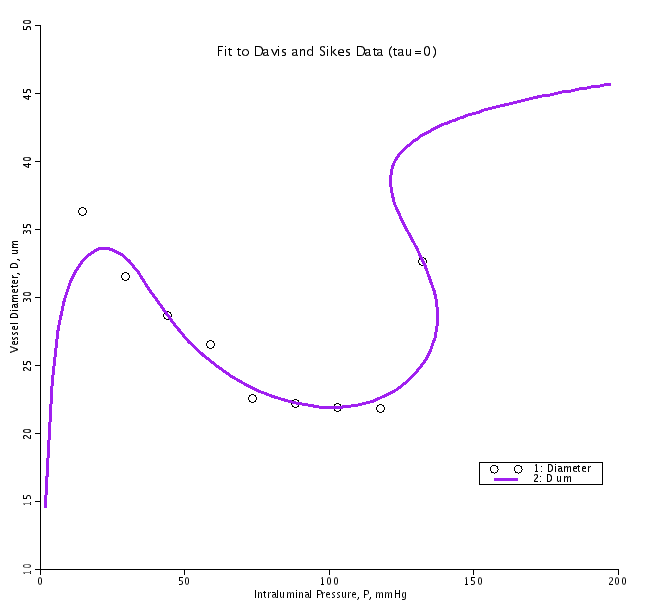
The vessel that is fit by the parameters used in this code is from the data presented in Figure 3 of a study by Davis MJ and Sikes PJ, Amer J Physiol Heart Circ Physiol 259:H1890-H1900, 1990. Other data sets can be fit using different values of C_p1, C_p2, C_a1, C_a2, C_a3, C_myo, C_tone and C_shear.