Models uptake of tracer potassium by skeletal muscle during continuous perfusion, flow constant or varied. Estimates the PS for the single composite barrier between axially distributed plasma and the cell potassium pool. (derived from model 0080)

Description

This model describes the exchange of potassium between capillary blood and the cells of skeletal muscle in dogs. The data and an initial formulation of the model come from the classic papers of Eugene Renkin (1959a,b). They are classic because these two papers introduced the idea of exchange along the length of the capillary and summarized the notion of transcapillary extraction as being interpretable quantitatively in terms of the relationship between blood flow, F ml/(g*min), and the permeability-surface area product, PS ml/(g*min). The permeability, P cm/min, and the capillary surface area, S cm²/(g.tissue), are an inseparable product defining an overall conductance for a solute. Extraction, E, in these papers is defined as the difference in the steady state between the arterial solute concentration [A] and the venous concentration [V] of the extracted solute: divide by [A]:

        E = ( [A] - [V] ) / [A]   which is dimensionless.                                (1)

The extraction, measured by using radioactive tracer potassium, K-42, was interpreted as if there were no return flux of K-42 from tissue back into the capillary blood, and which, if true, the unidirectional flux of solute from blood to tissue must be the extraction times the flow of solute entering the capillary:

        Solute flux = E * [A] * F    moles/(g*min).                                      (2)

Renkin's model ignored the "back-diffusion" or return flux that showed in his data, but which he recognized. While he appreciated from his earlier work with Pappenheimer (1951) the porosity of the endothelial barrier, the steady-state data of this experiment did not allow him to consider separately the interstitial space or the endothelial cells and periendothelial cellular clefts or the muscle cell membrane,so he lumped them together as a composite membrane. He derived the classic equation for the extraction along a single axially distributed capillary or pipe with axially uniform permeability:

        E = 1 - exp(-PS/F)                                                               (3)

which in turn provided a direct way of estimating PS from the data:

        PS = - F ln (1-E)   ml/(g*min).                                                  (4)

Christian Crone (1963,1965) in his thesis derived the same equations, but instead of performing steady state state (step response ) experiment, used bolus injections of tracer (impulse response). Most importantly, Crone sharpened the interpretation of the data by including an intravascular reference tracer so that the extraction was defined much precisely than the arteriovenous difference:

        E(t)  =  1 - h_d(t)/ h_R(t)                                                      (5)

at each point in time, where h(t) is the fraction of the injected dose (of either the diffusible tracer, d, or of the reference intravascular tracer R) appearing at the outflow per second,

        h(t)  = F * C(t) / q0                                                            (6)

where q0 is the injected dose, moles, and C(t) is the concentration-time curve at the outflow, M.

He focused on the early upslope of the extraction curve so that it represented a unidirectional flux from blood to tissue uncontaminated by an return flux from tissue to blood. Neither of them appreciated at that time that Christian Bohr had developed the same equations in 1909 to explain alveolar capillary exchange, or that Sangren and Sheppard (1954) had developed a fully mass-conservative model accounting for return flux from tissue to capillary. Renkin was troubled by the difference between his skeletal muscle data and those on the heart (Conn and Robertson 1955), but the cause of the difference was really that myocardial flows are 50 to 100 times higher in the heart since it is a working muscle. Sheehan and Renkin (1972) reanalyzed these data later with a more refined model accounting for the endothelial and parenchymal barriers as different entities.

Crone's impulse response experiment allowed a clear estimate of the PS for the endothelial barrier: the high flow and higher resolution data allowed him to obtain an estimate of E before there was backflux from the ISF. This was the technique used by Yipintsoi (1970) to estimate capillary PS in the heart, and Tancredi (1975) to estimate the endothelial PS and the muscle cell PS separately. Thus Crone's work and Renkin's were nicely complementary, and their quiet rivalry for priority ignored the fact that they had long since been scooped by Bohr, and out-quantitated by Charles Sheppard. Crone's high resolution method allowed refined questions concerning the nature of the cleft wides between endothelial cells (Crone 1963), showing the lack of steric hindrance in transendothelial passage and thereby challenging the Pappenheimer portrayal that the clefts were of the order of only 5 nanometers. Later work on heart suggested that the clefts are closer to 14nm wide Kellen (2002a,b).

Renkin was interested in the regulation of flow to the muscle and in the exchangeability of muscle solutes. The data showed two features that stimulated his later research: One was that the PS diminishedwhen flow F was reduced and increased with increasing F, as if more of the vascular bed opened up at higher pressures and flows, which is true. This raised the question of regional flow heterogeneity. His earlier studies (1955) had also alerted him to this idea that perfusion was not uniform throughout a muscle, and in later studies he explored further (Renkin and Rosell 1962), but this was before the development of particle deposition techniques to show regional perfusion heterogeneity in a quantitative fashion.

The model provided here goes beyond Renkin's who limited himself to the interpretation of the experimentally measured A-V extraction, E, but the model is still grossly oversimplified, consisting of only 2 region in N axially-distributed capillary-tissue exchange unit, and assuming a composite membrane between blood and cell. There is an inflow pipe to represent the cannula into the arterial inflow. The capillary tissue unit provides for the equations above and in addition gives measures of the return flux from tissue to blood and the estimation of the potassium content of the cells or the "exchangeable fraction" of cell potassium. This component of the model is the same as the Sangren-Sheppard model with full mass balance, plus accounting for the inevitable degree of dispersion of solute along the length of the capillary, as in the model of Bassingthwaighte (1974).

This simple model provides a good fit to the data of Fig 1A (1959a) as shown in the FIGURE (webfig to duplicate first plot page), but required reducing the size of the estimated potassium pool that is rapidly exchangeable with blood potassium. Renkin observed that with higher flows the exchangeable fraction is larger, and the PS's are higher, as if more capillaries are open. Might there be a consistent relationship such that PS increases with flow, F? The explanation really demands deeper modeling, not only with respect to capillary perfusion heterogeneity and PS but also other issues: (1) tracer K-42 was added to a volume of blood used as perfusate so that K-42 could enter RBC gradually in this supply source and then comprise an increasing fraction of intra-erythrocyte K-42 which would be slowed in reaching the cells compared to plasma K-42; (2) the interstitial of K-42 pool is always bigger than the plasma pool and so constitutes both a delay for tracer and a source of relatively rapid reflux; and (3) in skeletal muscle cells of diameters about 50 microns or so there must be substantial diffusional retardation to exchange and the "rapidly exchangeable fraction" is at the periphery of the cell. Such hypotheses can be tested by extending the model to represent each of these features.

In Summary, the Renkin (1959) and Crone (1963) methods for estimating PS are complementary, Renkin using a pseudo-steady-state step or constant infusion response, and Crone using a bolus injection brief pulse response. By Renkin's method the measured E is a net extraction where return flux from the cell is slow but return flux from ISF is relatively fast and is not observable distinctly. The Crone method has high temporal resolution for estimating the initial loss across the endothelial barrier alone, and E is effectively a measure of unidirectional flux. The Crone method is clearly better for studies of mechanisms of trans-endothelial transport in capillary-tissue exchange.

Model implementation details:

    An entry spatial domain, z, accounts for delay in the cannula leading
to the arterial inflow. Model is an axially distributed pipe, BTEX10, with its 
dispersion controlled by the dispersion coeffient, Dz. 
   These partial differential equations model a "tissue cylinder" 
consisting of two regions, the capillary plasma, p, and parenchymal cell, pc.  
The PS is that for a composite membrane with components in series (endothelium, 
ISF, cell membrane). This is a tracer experiment so that chemical concentrations 
do not change, and PS is not dependent on tracer concentration ir on the 
mechanism of its conductance.
    Isotopic decay is not the cause of the diminution in the inflow
concentration: Renkin states (1959a) that the data have all been
corrected for the decay. (The half life of K42 is 12.44 hours.) 

  The first data set from Renkin 1959a, Figure 1A, has flow 1.36 to 1.38 ml/min
for a 11.2 g muscle, 0.122 ml/(g*min). (Set this in "scale" with fgen2 Amp=1.)
   Renkin's expt P26 was estimated to have PS = 4.8 ml / (min* 100 g) at a flow of 
10 ml/(min*100g), while the solution modeled above with no PS flow dependence (A2=0) 
estimated it to be 0.091 ml/(g*min) or 9.1 ml / (min* 100g) at a flow of 
12.1 ml/(min*100g). Our calculated theoretical PS (PStheor) is 0.046 ml/(g*min) 
or 4.6 ml/(min*100g). Renkins estimate was interpolated from the clearance of K+ at many flows.
Renkin's estimate does not explicitedly take into account back-diffusion of K+
back into the capillary but rather adds a correction to the outflow K42 counts
based on injection of tracer free blood afterwards and the outflow activity at that
point is considered due to back-diffusion.

 When PS flow dependence is added and our solution fitted to variable 
flow data (Renkin 1959a Figure 1B, expt P27, Load and run parameter set 'Fig1B') 
the estimated PS is 0.033 ml/(g*min) or 3.3 ml/(min*100g) at a flow of 
9.7 ml/(min*100g). Renkin's interpolated PS estimate was 6.4 ml/(min*100g) at 
flow of 10 ml/(min*100g). Renkin's PS estimate corresponds to the Maximum PStheor 
value from our model of 6.8 ml/(min*100g). If we turn off flow dependence (A2=0 and A1=1) we get 
estimated PS of 3.2 ml/(min*100g) showing very little PS flow dependence at flows 
modeled here (As the model stands, there is high correlation between A1, A2 and PS0).

The flow dependence coefficients A1 and A2 relate to the physiology in terms of 
vascular perfusion. A1 relates to regions well perfused and should be set to 1 or zero
while A2 represents regions initially poorly perfused but as arterial pressure increases, 
blood flow through the capillaries of poorly perfused regions increase more rapidly 
then those regions already well perfused (Renkin 59b paper). The Renkin data presented 
here shows little flow dependence (Set A2=0 and A1=1 and fit Fig1B data to confirm).
 

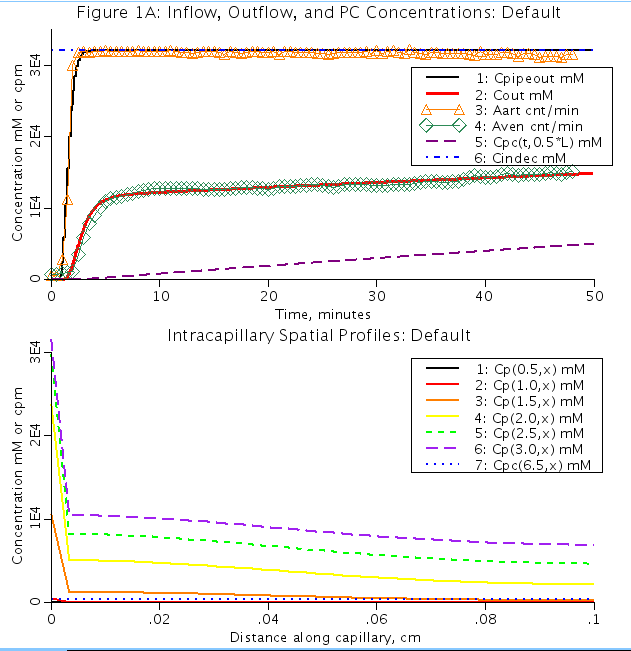
Figure: (Top): Two region model fit to Renkin 1959a potassium tracer K+⁴²,data (Aart:orange triangles and Aven:green diamonds).
Outflow from capillary pipe (Cout) is fit to Avent and concn out from cannula into artery (Cpipeout) is fit to Aart data.
Cpc is the concentration of K+ in the parencyhmal cell region (outside of the pipe). Cindec is the concentration of
K+ coming into the pipe. (Bottom): Spatial profiles of the conentration of K+ along the pipe at different time intervals.
Cpc is the concentration of K+ in the parenchymal cell at time, t=6.5 min.

Equations

The equations for this model may be viewed by running the JSim model applet and clicking on the Source tab at the bottom left of JSim's Run Time graphical user interface. The equations are written in JSim's Mathematical Modeling Language (MML). See the Introduction to MML and the MML Reference Manual. Additional documentation for MML can be found by using the search option at the Physiome home page.