The Sangren-Sheppard model (Bull Math Biophys 15: 387-394, 1953) for the exchange of a labeled substance between a liquid flowing in a vessel and an external compartment. Similar to BTEX20 with no diffusion

Description

    The Sangren-Sheppard model may be seen as a varient of the btex20_pde
model. Instead of specifying Vp, Visfp, and PSg, three alternative 
parameters are specified, (1) tcap, the capillary transit time, (2) gamma,
the ratio of Visfp to Vp, and (3) psf, the ratio of of PSg to Fp (flow).
Vp, Visfp, and PSg are then given by

    Vp=Fp*tcap, Visfp=gamma*Vp, and PSg=psf*Fp. Once these parameters
are calculated, the model is the same as btex20_pde with out diffusion.

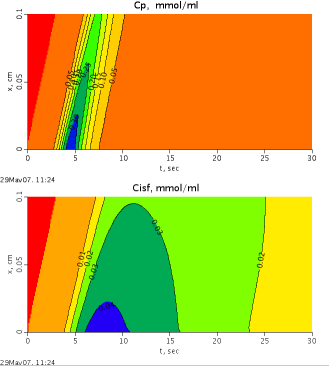
    This is a model of a "tissue cylinder" consisting of a capillary 
plasma region and an interstitial fluid (isf) region. The model is 
multi-segmented in a single spatial dimension to solve the convection-
diffusion equation with exchange and consumption. It is modeled as a 
differential equation coupled with an ordinary differential equation. 

    The convecting plasma region has volume Vp, flow Fp, first order 
consumption coefficient Gp. The interstitial fluid (isf) region has volume 
Visfp, first order consumption coefficient Gisf. The name of the 
isf volume, Visfp, is derived from Visf' where the prime is rendered as p.  
The isf volume is a volume of distribution which might or might not 
correspond to a physical volume. It is referred to as a virtual volume. 
PS is the permeability surface product of the membrane. It is also 
known as PScap (PS for the CAPillary region) and PSg (the PS for the 
Gap between endothelial cells which allows for the passive exchange of 
material between the plasma and the isf. In this model, the PS is denoted 
PSg. In other nomenclature it is denoted PSc where c stands for "cleft", 
a synonym for gap.

     Units are per gram of tissue (physiological) so that a single sanshe
unit can model a homogeneously perfused organ. 

     Instantaneous mixing is assumed in each individual segment in each
region. Passive exchange between plasma and isf regions has conductance
PSg. 

     This model can be adapted and expanded to represent multi-capillary
models in serial and parallel configurations.

Equations

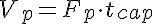
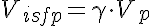
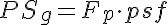
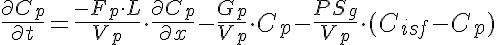
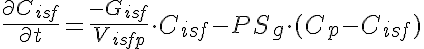
Initial Conditions:
 

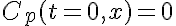
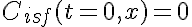
Boundary Conditions:

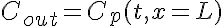
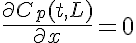
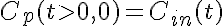
The equations for this model may be viewed by running the JSim model applet and clicking on the Source tab at the bottom left of JSim's Run Time graphical user interface. The equations are written in JSim's Mathematical Modeling Language (MML). See the Introduction to MML and the MML Reference Manual. Additional documentation for MML can be found by using the search option at the Physiome home page.