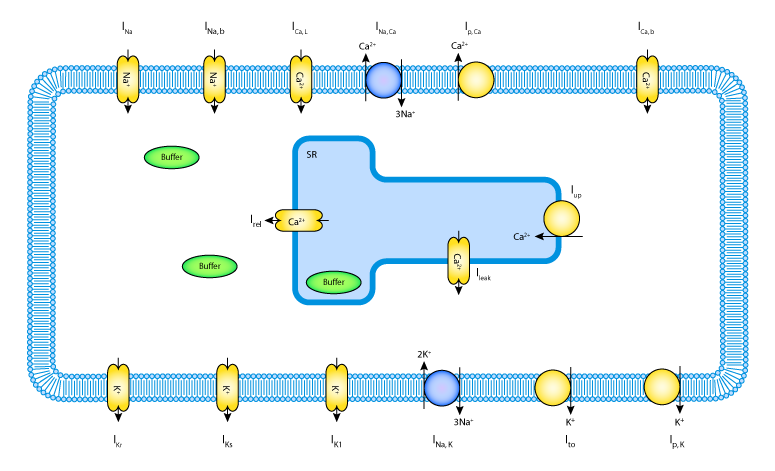
This model simulates the action potential for a human ventricular myocyte accounting for Na, K and Ca transport and dynamics.

Description

   This model simulates the electrophysiology of a single cardiomyocyte taking into 
   consideration selected Na, K and Ca transport along with Ca shuttling between the
   sarcoplasmic reticulum (SR) and cytosol, and buffering of Ca in both cytosol and
   SR.  The model is based on the study by ten Tusscher et al. (Amer J Physiol 286:
   H1573-H1589, 2004).  This version documents the changes made after downloading the 
   JSim model from:

www.physiome.org/jsim/models/cellml/#tentusscher_noble_noble_panfilov_2004

   and modifying it to run in with unit checking enabled.  A comparison to the 
   same model running in the CellML simulation suite PCEnv which was downloaded from:

www.cellml.org/models/tentusscher_noble_noble_panfilov_2004

   enabled the following changes to be made:

	1) The membrane capacitance is not used in the equation for dV/dt since
	   the currents are already given in units of pA/pF which would indicate
	   capacitance has already been factored in.  Therefore the expression used in
	   this simulation is:

                  dV/dt = -1 * ( i_ion + i_stim )

 	   instead of:

		    dV/dt = -1 * ( i_ion + i_stim ) / Cm

	   which is given in the original paper.

	2) Membrane reversal potentials are incorrectly presecribed as log(Co/Ci) 
 	   (base 10) instead of ln(Co/Ci) in the CellML version 1 that is used
	   to generate the JSim project file.

	3) A different expression is used for the rate of change of gating parameters
	   used for fast Na m, h and j gate, L-type Ca d gate, slow delayed rectifier
	   K Xs gate, rapid delayed rectifier K Xr1 and Xr2 gate.  In CellML version 
           1 they were specified as:

		    dx/dt = alpha_x * (1 - x) + beta_x * x

	   while in the PCEnv version 

		    dx/dt = (x_infinity - x ) / tau_x

	   is used where x is the gating variable

	4) Error in the Ca dependent inactivation gate for L-type Ca channel
	   calculation involving alpha_fCa.  In version 1 used for JSim:
		
		    alpha_fCa = 1 / (1 + exp((Cai / (3.25E-4 mM))^8)) 

	   whereas in the PCEnv version:

		    alpha_fCa = 1 / (1 + ((Cai / (3.25E-4 mM))^8))	    

	   is used.

	5) Incorporation of different Ca dynamics expressions that existed in the
	   PCEnv version but were not documented in the original paper or used in
	   the JSim version.  In the paper buffering was calculated but did not 
	   factor in the calcium dynamics.  Also in order to convert the Ca currents
	   into Ca fluxes the membrane capacitance must be included but was not. The 
	   equations out of the paper and used in CellML version 1 are:

	   	    Cai_bufc = Cai * Bufc / (Cai + Kbufc)
 		    Casr_bufsr = CaSR * Bufsr / (CaSR + Kbufsr)
		    Cai:time = ((i_CaL + i_bCa + i_pCa - (2*i_NaCa)) / (2*Vc*F))
		                  + i_leak - i_up + i_rel;
		    CaSR:time = (Vc/Vsr) * (i_up - i_rel - i_leak)

	   where the following equations are used in PCEnv:

		    Cai_bufc = 1 / (1 + (Bufc * Kbufc) / ((Cai + Kbufc)^2))
		    Casr_bufsr = 1 / (1 + (Bufsr * Kbufsr)/ ((CaSR + Kbufsr)^2))
		    Cai:time = Cai_bufc * (i_leak - i_up + i_rel
                        - Cm  * ((i_CaL + i_bCa + i_pCa - (2*i_NaCa)) / (2*Vc*F)))
		    CaSR:time = Casr_bufsr * (Vc/Vsr) * (i_up - i_rel - i_leak)

	6) Also Na and K dynamics were altered to take into consideration the 
	   membrane capacitance.  The CellML version 1 and original paper 
	   equations are:

		    
		    Nai:time = -1 * (i_Na + i_bNa + (3*i_NaK) 
					+ (3*i_NaCa)) / (Vc*F)
		    Ki:time = -1 * (i_K1 + i_to + i_Kr + i_Ks + i_pK
		    		+ i_stim + i_pK - (2*i_NaK) - i_ax) / (Vc*F) 

	   where the PCEnv simulation uses

		    Nai:time = -Cm * (i_Na + i_bNa + (3*i_NaK) 
					+ (3*i_NaCa)) / (Vc*F)
		    Ki:time = -Cm * (i_K1 + i_to + i_Kr + i_Ks + i_pK 
					+ i_stim - (2*i_NaK)) / (Vc*F)

Equations

Equations for this model are presented in the AJP article with the following additions and exceptions:

1. Currents are represented in pA/pF therefore membrane capacitance has already been taken into account in the expression for dV/dt
2. Calcium dynamics equations have been changed to include dependence on buffering.
3. Ca, Na and K dynamics now account for membrane capacitance.
4. The rate of change of all gating variables is:

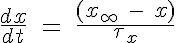
unless indicated otherwise in paper.

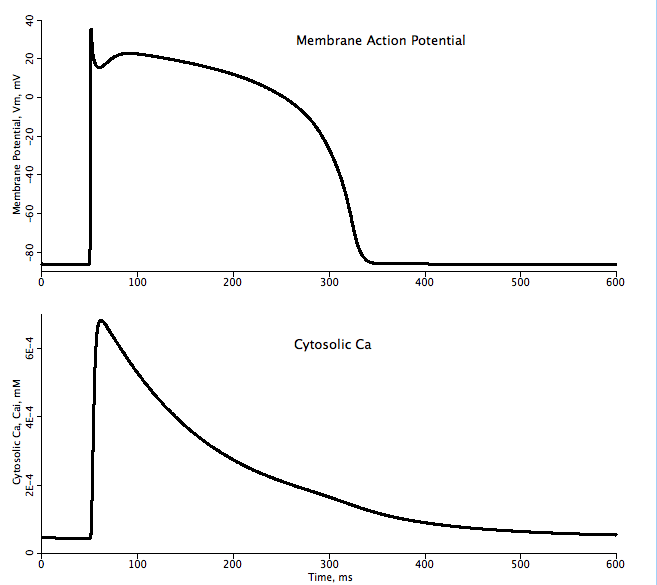
The parameters and equations used in this model are for the epicardial myocyte variant to match the graphs given in Figure 7.

For more details please look at notes in JSim model source code.

The equations for this model may be viewed by running the JSim model applet and clicking on the Source tab at the bottom left of JSim's Run Time graphical user interface. The equations are written in JSim's Mathematical Modeling Language (MML). See the Introduction to MML and the MML Reference Manual. Additional documentation for MML can be found by using the search option at the Physiome home page.