(Matlab) Dynamics of cross-bridge cycling, ATP hydrolysis, force generation, and deformation in cardiac muscle.

Description

(Abstract) Despite extensive study over the past six decades the coupling of chemical reaction and mechanical processes in muscle dynamics is not well understood. We lack a theoretical description of how chemical processes (metabolite binding, ATP hydrolysis) influence and are influenced by mechanical processes (deformation and force generation). To address this need, a mathematical model of the muscle cross-bridge (XB) cycle based on Huxley's sliding filament theory is developed that explicitly accounts for the chemical transformation events and the influence of strain on state transitions. The model is identified based on elastic and viscous moduli data from mouse and rat myocardial strips over a range of perturbation frequencies, and MgATP and inorganic phosphate (Pi) concentrations. Simulations of the identified model reproduce the observed effects of MgATP andMgADP on the rate of force development. Furthermore, simulations reveal that the rate of force re-developmentmeasured in slack–restretch experiments is not directly proportional to the rate of XB cycling. For these experiments, the model predicts that the observed increase in the rate of force generation with increased Pi concentration is due to inhibition of cycle turnover by Pi. Finally, the model captures the observed phenomena of force yielding suggesting that it is a result of rapid detachment of stretched attached myosin heads.

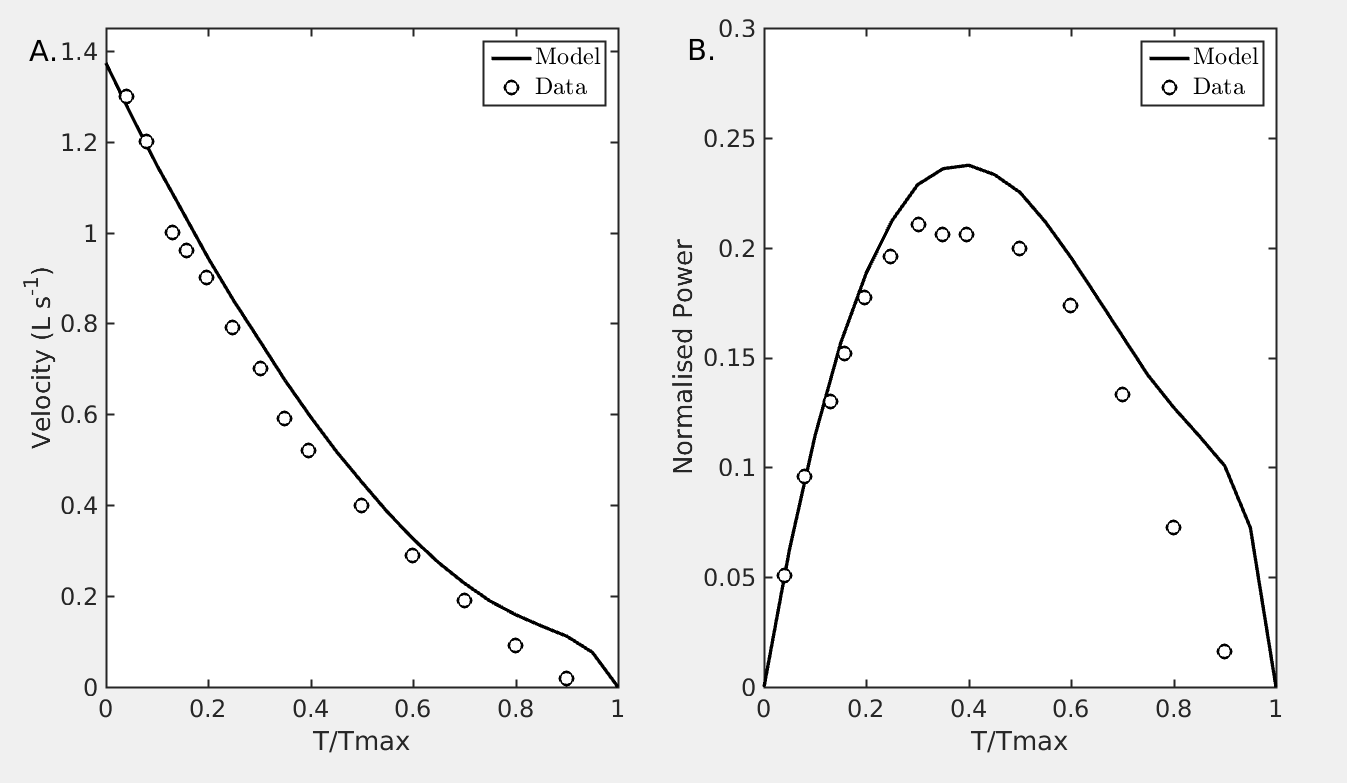
Figure 1: (Fig. 4 of Tewari et al. 2016 paper). Force–velocity relationship in mouse cardiacmuscle. (A.) Open circles are force–velocity data from Palmer et al. 2013 for control mouse myocardial strips. Solid line representsmodel simulations reproducing the experiments. Model based force–velocity data are computed by performing (computational) sarcomere quick-release experiments by holding the (virtual) sarcomere constant at a fixed length (2.2 μm) till maximumisometric tension (Tmax) is developed and velocitywas computed fromthe slope of percent SL change after ~45ms of release. After release the sarcomere wasmade to contract against different loads (T) less than equal to Tmax. For simulating the sarcomere release experiments the parallel linear spring is replaced by a non-linear spring as described by [Rice et al. 2008] and force due to this spring is set to be β ⋅ kPE,2, where β is a scaling factor chosen such that simulated unloaded shortening velocity matches experimentally reported value. For all the (computational) experiments, force due to this Rice-type spring is β ⋅ kPE,2. All other parameters are as reported in Table 1 for mouse. (B.) Normalized power is the product of (T/Tmax) × Velocity (L·s−1)

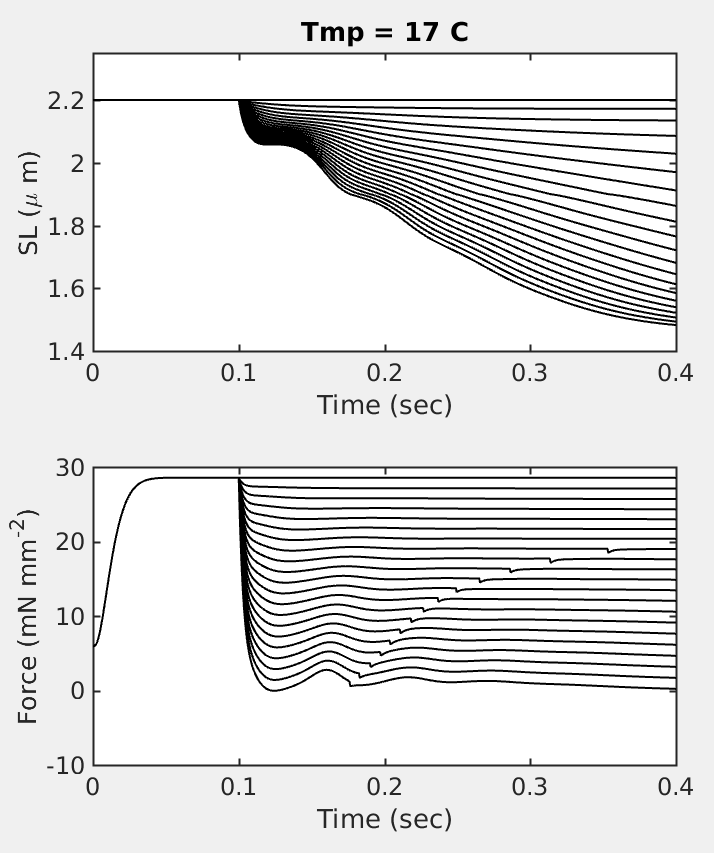
Figure 2: (A.) Representative sarcomere quick-release (computational) experiment with constant afterload. Increasing value of afterload decreases the amount sarcomere can contract. SL is sarcomer length. Note time-point (~ 0.15 sec) around which slopes were computed and an average of those slopes is reported as the shortening velocity. (B.) Total force on sarcomere as a function of time (myofibril + active + passive force).

Equations

The equations for this model may be viewed by opening up the Matlab model files downloaded from below.

Download Matlab model and associated files

• Matlab files (zip file)270.07 KB
• Description of model code276.53 KB
• Authors' website (more info)