Uses a single capillary convection diffusion model to generate functions of linear stationary systems: h(t), H(t), R(t), eta(t).
Description
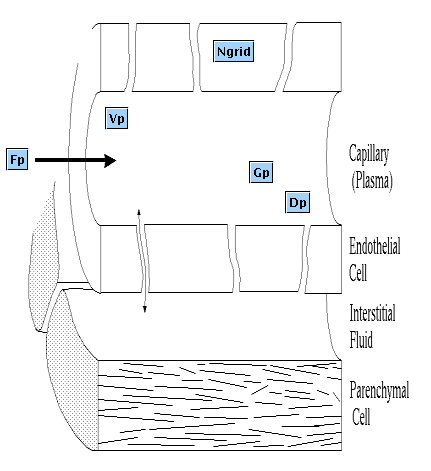 This partial differential equation models a "tissue cylinder" consisting of a single capillary, and is mathematically like BTEX10. The model has been parameterized to produce the operator functions from the Terminology paper of Bassingthwaighte et al.(1986). wIth a Dirac delta function input (unity area, input at t = 0) the response functions are: h(t) is the transport function (or transfer function) the probability density function of arrival times at the outflow, fraction of dose per second. H(t) is the cumulative residence time distribution function, and equals the fraction of the dose accumulated in a bucket at the outflow. R(t) is the residue function, the fraction of the injected mass retained in the system at time t. eta(t) is the emergence function or the fractional escape rate, the fraction of the retainied mass emerging from the outflow per second. It is equivalent to the risk function of the life insur=ance industry, the risk of dying at age t. Three situations are illustrated: 1. A general situation described above. Plot TERM, Parameter set Term. This uses a very short pulse injection. A modest diffusion coefficient illustrates the standard. If D is small the output is a delayed pulse, but numerical inaccuracies distort a very narrow pulse; for D > 0 the outflow, h(t), is nearly a Gaussian pdf, as exemplified by the closeness of fit of the spatial distribution by a Gaussian density funnction, on the spatial plot, SPACE. 2. A stirred tank. Use plot TANK and parameter set Tank. The ridiculously high diffusion coefficient disperses the matrial almost uniformly throughout the lngth of the tube, approximiating a stirred tank within the axially distributed region. The downslope of h(t) and of R(t) are almost monoexponenetial with time constabt = V/F. 3. a dispersed input function. USe plot DISP and parameter set Disp. Becasue the input is not a DIrac delta function the responses are not formally the "transport function", h(t), H(t), R(t), and eta(t), but are the delayed equivaalents. Using a lagged normal density function as input avoids the sharp discontinuities so that the numerical methods work better. (The equations are not so "stiff".)
This partial differential equation models a "tissue cylinder" consisting of a single capillary, and is mathematically like BTEX10. The model has been parameterized to produce the operator functions from the Terminology paper of Bassingthwaighte et al.(1986). wIth a Dirac delta function input (unity area, input at t = 0) the response functions are: h(t) is the transport function (or transfer function) the probability density function of arrival times at the outflow, fraction of dose per second. H(t) is the cumulative residence time distribution function, and equals the fraction of the dose accumulated in a bucket at the outflow. R(t) is the residue function, the fraction of the injected mass retained in the system at time t. eta(t) is the emergence function or the fractional escape rate, the fraction of the retainied mass emerging from the outflow per second. It is equivalent to the risk function of the life insur=ance industry, the risk of dying at age t. Three situations are illustrated: 1. A general situation described above. Plot TERM, Parameter set Term. This uses a very short pulse injection. A modest diffusion coefficient illustrates the standard. If D is small the output is a delayed pulse, but numerical inaccuracies distort a very narrow pulse; for D > 0 the outflow, h(t), is nearly a Gaussian pdf, as exemplified by the closeness of fit of the spatial distribution by a Gaussian density funnction, on the spatial plot, SPACE. 2. A stirred tank. Use plot TANK and parameter set Tank. The ridiculously high diffusion coefficient disperses the matrial almost uniformly throughout the lngth of the tube, approximiating a stirred tank within the axially distributed region. The downslope of h(t) and of R(t) are almost monoexponenetial with time constabt = V/F. 3. a dispersed input function. USe plot DISP and parameter set Disp. Becasue the input is not a DIrac delta function the responses are not formally the "transport function", h(t), H(t), R(t), and eta(t), but are the delayed equivaalents. Using a lagged normal density function as input avoids the sharp discontinuities so that the numerical methods work better. (The equations are not so "stiff".)
Equations
Differential Equations
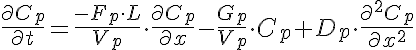
Left Boundary Conditions
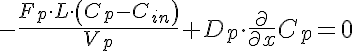
Right Boundary Conditions
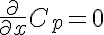 ,
, 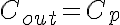
Initial Conditions
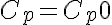 or
or 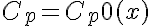
The equations for this model may be viewed by running the JSim model applet and clicking on the Source tab at the bottom left of JSim's Run Time graphical user interface. The equations are written in JSim's Mathematical Modeling Language (MML). See the Introduction to MML and the MML Reference Manual. Additional documentation for MML can be found by using the search option at the Physiome home page.
- Download JSim model MML code (text):
- Download translated SBML version of model (if available):
- No SBML translation currently available.
- Information on SBML conversion in JSim
We welcome comments and feedback for this model. Please use the button below to send comments:
Key reference: J.B. Bassingthwaighte, F.P. Chinard, C. Crone, C.A. Goresky, N.A. Lassen, R.S. Reneman, and K.L. Zierler. Terminology for mass transport and exchange. Am. J. Physiol. 250 (Heart. Circ. Physiol. 19): H539-H545, 1986. Selected early references on convection -diffusion situations: Taylor G. Dispersion of soluble matter in solvent flowing slowly through a tube. Proc R Soc Lond A 219: 186-203, 1953. Taylor G. The dispersion of matter in turbulent flow through a pipe. Proc R Soc Lond A 223: 446-468, 1954. Danckwerts PV. Continuous flow systems: Distribution of residence times. Chem Eng Sci 2: 1-13, 1953. Andres R, Zierler KL, Anderson HM, Stainsby WN, Cader G, Ghrayyib AS, and Lilienthal JL Jr. Measurement of blood flow and volume in the forearm of man; with notes on the theory of indicator-dilution and on production of turbulence, hemolysis, and vasodilatation by intra-vascular injection. J Clin Invest 33: 482-504, 1954. Meier P and Zierler KL. On the theory of the indicator-dilution method for measurement of blood flow and volume. J Appl Physiol 6: 731-744, 1954. References for Operational Analysis: Zierler KL. Theoretical basis of indicator-dilution methods for measuring flow and volume. Circ Res 10: 393-407, 1962. Cox DR. Renewal Theory. New York: Wiley, 1962, 142 pp. Other references re Convection Diffusion W.C. Sangren and C.W. Sheppard. A mathematical derivation of the exchange of a labelled substance between a liquid flowing in a vessel and an external compartment. Bull Math BioPhys, 15, 387-394, 1953. C.A. Goresky, W.H. Ziegler, and G.G. Bach. Capillary exchange modeling: Barrier-limited and flow-limited distribution. Circ Res 27: 739-764, 1970. J.B. Bassingthwaighte. A concurrent flow model for extraction during transcapillary passage. Circ Res 35:483-503, 1974. B. Guller, T. Yipintsoi, A.L. Orvis, and J.B. Bassingthwaighte. Myocardial sodium extraction at varied coronary flows in the dog: Estimation of capillary permeability by residue and outflow detection. Circ Res 37: 359-378, 1975. C.P. Rose, C.A. Goresky, and G.G. Bach. The capillary and sarcolemmal barriers in the heart--an exploration of labelled water permeability. Circ Res 41: 515, 1977. J.B. Bassingthwaighte, C.Y. Wang, and I.S. Chan. Blood-tissue exchange via transport and transformation by endothelial cells. Circ. Res. 65:997-1020, 1989. Poulain CA, Finlayson BA, Bassingthwaighte JB.,Efficient numerical methods for nonlinear-facilitated transport and exchange in a blood-tissue exchange unit, Ann Biomed Eng. 1997 May-Jun;25(3):547-64.
Please cite https://www.imagwiki.nibib.nih.gov/physiome in any publication for which this software is used and send one reprint to the address given below:
The National Simulation Resource, Director J. B. Bassingthwaighte, Department of Bioengineering, University of Washington, Seattle WA 98195-5061.
Model development and archiving support at https://www.imagwiki.nibib.nih.gov/physiome provided by the following grants: NIH U01HL122199 Analyzing the Cardiac Power Grid, 09/15/2015 - 05/31/2020, NIH/NIBIB BE08407 Software Integration, JSim and SBW 6/1/09-5/31/13; NIH/NHLBI T15 HL88516-01 Modeling for Heart, Lung and Blood: From Cell to Organ, 4/1/07-3/31/11; NSF BES-0506477 Adaptive Multi-Scale Model Simulation, 8/15/05-7/31/08; NIH/NHLBI R01 HL073598 Core 3: 3D Imaging and Computer Modeling of the Respiratory Tract, 9/1/04-8/31/09; as well as prior support from NIH/NCRR P41 RR01243 Simulation Resource in Circulatory Mass Transport and Exchange, 12/1/1980-11/30/01 and NIH/NIBIB R01 EB001973 JSim: A Simulation Analysis Platform, 3/1/02-2/28/07.

