Model for slow ligand binding to 4 independent non-cooperative, identical, sites without reaction.
Description
A protein with 4 independent binding sites, without cooperatively, can be empty or fully
saturated with a ligand, i.e., all of its binding sites can be occupied at high
concentrations. The fractional saturation is calculated here by three similar means,
and compared with the result using a Hill coefficient of 2.7. The value is chosen
because the Hill equation with nH = 2.7 fits oxyhemoglobin saturation curves well.
The math is based on the equation for single site binding, modified
in recognition that there are 4 sites available to fill, and when
one is filled, only 3 remain, reducing the odds from 4 to 3, and so on. The generic
substrate is represented here by the liganding molecule O2 and the 4- binding site protein
by Hb. Fully occupied oxyhemoglobin is Hb(O2)_4. In the model, the notation HbO = Hb(O2)_1,
HbO2 = Hb(O2)_2, etc. At any given ligand concentration all 5 forms of Hb may exist: Hb, HbO,
HbO2, HbO3, and HbO4. The sum of the products of the relative concentrations of each of
these times the # of ligands being carried in each form is divided by 4 gives the fractional
saturation, SHb.
This model serves as a basis of cooperativity models wherein the filling of the
first and successive sites causes (by cooperativity = positive feedback through
molecular conformational rearrangement) successively higher affinities. See Hbcoop.proj, #30.
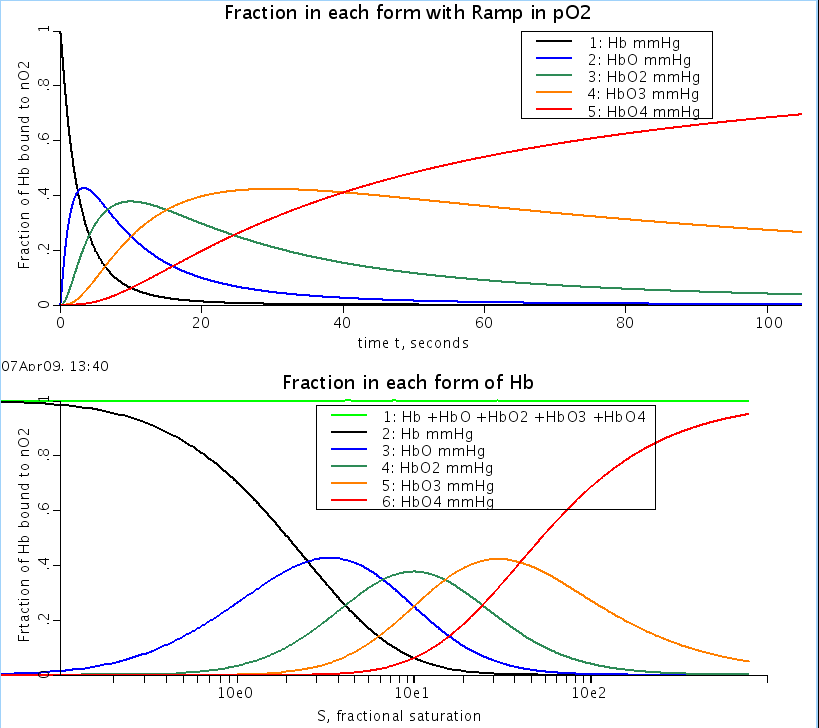
Figure: Fraction of bound hemoglobin:
Equations
The equations for this model may be viewed by running the JSim model applet and clicking on the Source tab at the bottom left of JSim's Run Time graphical user interface. The equations are written in JSim's Mathematical Modeling Language (MML). See the Introduction to MML and the MML Reference Manual. Additional documentation for MML can be found by using the search option at the Physiome home page.
- Download JSim model MML code (text):
- Download translated SBML version of model (if available):
We welcome comments and feedback for this model. Please use the button below to send comments:
Hill AV: The diffusion of oxygen and lactic acid through tissues. Proc R Soc Lond (Biol) 104: 39-96, 1928. Adair GS: The hemoglobin system. VI. The oxygen dissociation curve of hemoglobin. J Biol Chem 63: 529-545, 1925. Hill AV: The possible effects of the aggregation of the molecules of haemoglobin on its dissociation curves. J Physiol 40: iv-vii, 1910 Hill R: Oxygen dissociation curves of muscle hemoglobin. Proc Roy Soc Lond B 120: 472-480, 1936. Keener J and Sneyd J: Mathematical Physiology. New York, NY: Springer-Verlag, 1998, 766 pp. Roughton FJW, Deland EC, Kernohan JC, and Severinghaus JW: Some recent studies of the oxyhemoglobin dissociation curve of human blood under physiological conditions and the fitting of the Adair equation to the standard curve. In: Oxygen Affinity of Hemoglobin and Red Cell Acid Base Status. Proceedings of the Alfred Benzon Symposium IV Held at the Premises of the Royal Danish Academy of Sciences and Letters, Copenhagen 17-22 May, 1971, edited by Rorth M and Astrup P. Copenhagen: Munksgaard, 1972, p. 73-81. Winslow RM, Swenberg M-L, Berger RL, Shrager RI, Luzzana M, Samaja M,and Rossi-Bernardi L: Oxygen equilibrium curve of normal human blood and its evaluation by Adair's equation. J Biol Chem 252: 2331-2337, 1977.
Please cite https://www.imagwiki.nibib.nih.gov/physiome in any publication for which this software is used and send one reprint to the address given below:
The National Simulation Resource, Director J. B. Bassingthwaighte, Department of Bioengineering, University of Washington, Seattle WA 98195-5061.
Model development and archiving support at https://www.imagwiki.nibib.nih.gov/physiome provided by the following grants: NIH U01HL122199 Analyzing the Cardiac Power Grid, 09/15/2015 - 05/31/2020, NIH/NIBIB BE08407 Software Integration, JSim and SBW 6/1/09-5/31/13; NIH/NHLBI T15 HL88516-01 Modeling for Heart, Lung and Blood: From Cell to Organ, 4/1/07-3/31/11; NSF BES-0506477 Adaptive Multi-Scale Model Simulation, 8/15/05-7/31/08; NIH/NHLBI R01 HL073598 Core 3: 3D Imaging and Computer Modeling of the Respiratory Tract, 9/1/04-8/31/09; as well as prior support from NIH/NCRR P41 RR01243 Simulation Resource in Circulatory Mass Transport and Exchange, 12/1/1980-11/30/01 and NIH/NIBIB R01 EB001973 JSim: A Simulation Analysis Platform, 3/1/02-2/28/07.

