Blood HbO2 and HbCO2 Dissociation Curves at Varied O2, CO2, pH, 2,3-DPG and Temperature Levels. Based directly on Dash et al. 2010 errata reprint.
Description
ABSTRACT: New mathematical model equations for O2 and CO2 saturations of hemoglobin (SHbO2 and SHbCO2)
are developed here from the equilibrium binding of O2 and CO2 with hemoglobin inside RBCs.
They are in the form of an invertible Hill-type equation with the apparent Hill coefficients
KHbO2 and KHbCO2 in the expressions for SHbO2 and SHbCO2 dependent on the levels of O2 and CO2
partial pressures (PO2 and PCO2), pH, 2,3-DPG concentration, and temperature in blood.
The invertibility ofmol2ml these new equations allows PO2 and PCO2 to be computed efficiently from
SHbO2 and SHbCO2 and vice-versa. The oxyhemoglobin (HbO2) and carbamino-hemoglobin (HbCO2)
dissociation curves computed from these equations are in good agreement with the published
experimental and theoretical curves in the literature. The model solutions describe that,
at standard physiological conditions, the hemoglobin is about 97.2% saturated by O2 and the
amino group of hemoglobin is about 13.1% saturated by CO2. The O2 and CO2 content in whole blood
are also calculated here from the gas solubilities, hematocrits, and the new formulas for SHbO2
and SHbCO2. Because of the mathematical simplicity and invertibility, these new formulas can be
conveniently used in the modeling of simultaneous transport and exchange of O2 and CO2 in the
alveoli-blood and blood-tissue exchange systems.
The equations for O2 and CO2 saturations of hemoglobin (SHbO2 and SHbCO2)
are derived by considering the various kinetic reactions involving the
binding of O2 and CO2 with hemoglobin in RBCs:
kf1p K1dp
1. CO2+H2O <--> H2CO3 <--> HCO3- + H+; K1=(kf1p/kb1p)*K1dp
kb1p K1 = 7.43e-7 M, K1dp = 5.5e-4 M
kf2p K2dp
2. CO2+HbNH2 <--> HbNHCOOH <--> HbNHCOO- + H+; K2=(kf2p/kb2p)*K2dp
kb2p K2 = 2.95e-5, K2dp = 1.0e-6 M
kf3p K3dp
3. CO2+O2HbNH2 <--> O2HbNHCOOH <--> O2HbNHCOO- + H+; K3=(kf3p/kb3p)*K3dp
kb3p K3 = 2.51e-5, K3dp = 1.0e-6 M
kf4p
4. O2+HbNH2 <--> O2HbNH2; K4p=K4dp*func([O2],[H+],[CO2],[DPG],T)
kb4p K4dp and K4p are to be determined
func = ([O2]/[O2]s)^n0*([H+]s/[H+])^n1*([CO2]s/[CO2])^n2*
([DPG]s/[DPG])^n3*(Temps/Temp)^n4
K5dp
5. HbNH3+ <--> HbNH2 + H+; K5 = 2.63e-8 M
K6dp
6. O2HbNH3+ <--> O2HbNH2 + H+; K6 = 1.91e-9 M
The association and dissociation rate constants of O2 with hemoglobin is
assumed to be dependent on [O2], [H+], [CO2], [DPG] and temperature (Temp)
such that the equilibrium constant K4p is proportional to ([O2]/[O2]s)^n0,
([H+]s/[H+])^n1, ([CO2]s/[CO2])^n2, ([DPG]s/[DPG])^n3, and (Temps/Temp)^n4.
The problem is to estimate the values of the proportionality constant K4dp
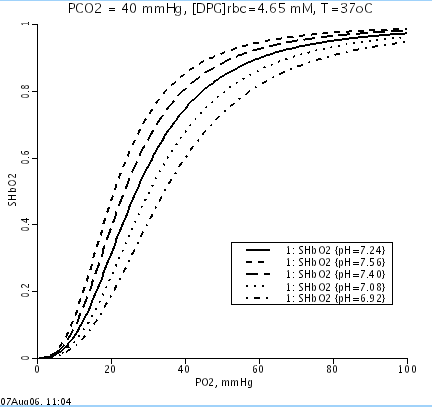
and the indices n0, n1, n2, n3 and n4 such that SHbO2 is 50% at pO2 = 26.8
mmHg, pH = 7.24, pCO2 = 40 mmHg, [DPG] = 4.65 mM and Temp = 37 C in RBCs
and the HbO2 dissociation curve shifts appropriately w.r.t. pH and pCO2.
Oxygen dissociation curves at varying pH:
Equations
The equations for this model may be viewed by running the JSim model applet and clicking on the Source tab at the bottom left of JSim's Run Time graphical user interface. The equations are written in JSim's Mathematical Modeling Language (MML). See the Introduction to MML and the MML Reference Manual. Additional documentation for MML can be found by using the search option at the Physiome home page.
- Download JSim model MML code (text):
- Download translated SBML version of model (if available):
We welcome comments and feedback for this model. Please use the button below to send comments:
Dash RK and Bassingthwaighte JB. Erratum to: Blood HbO2 and HbCO2 dissociation curves at varied O2, CO2, pH, 2,3-DPG and Temperature Levels. Ann Biomed Eng 38(4): 1683-1701, 2010.
Dash, R.K. and Bassingwaighte, J.B., Simultaneous Blood-Tissue Exchange of Oxygen, Carbon Dioxide, Bicarbonate, and Hydrogen Ion, Ann Biomed Eng, Vol 34:7 (Jul 2006) pp.1129-1148.
Please cite https://www.imagwiki.nibib.nih.gov/physiome in any publication for which this software is used and send one reprint to the address given below:
The National Simulation Resource, Director J. B. Bassingthwaighte, Department of Bioengineering, University of Washington, Seattle WA 98195-5061.
Model development and archiving support at https://www.imagwiki.nibib.nih.gov/physiome provided by the following grants: NIH U01HL122199 Analyzing the Cardiac Power Grid, 09/15/2015 - 05/31/2020, NIH/NIBIB BE08407 Software Integration, JSim and SBW 6/1/09-5/31/13; NIH/NHLBI T15 HL88516-01 Modeling for Heart, Lung and Blood: From Cell to Organ, 4/1/07-3/31/11; NSF BES-0506477 Adaptive Multi-Scale Model Simulation, 8/15/05-7/31/08; NIH/NHLBI R01 HL073598 Core 3: 3D Imaging and Computer Modeling of the Respiratory Tract, 9/1/04-8/31/09; as well as prior support from NIH/NCRR P41 RR01243 Simulation Resource in Circulatory Mass Transport and Exchange, 12/1/1980-11/30/01 and NIH/NIBIB R01 EB001973 JSim: A Simulation Analysis Platform, 3/1/02-2/28/07.

