This model simulates the competitive binding of two different enzymes which result in a similar product.
Description
This model represents the enzymatic conversion of a single substrate, S, to a single product, P by two competing enzymes. First a binding of the solute to an enzyme, E1 or E2, is achieved, which forms a substrate-enzyme complex, ES1 or ES2. The binding is followed by a reaction-release event, which yields the product and the enzyme. The entire binding-reaction-release sequence may be represented symbolically as
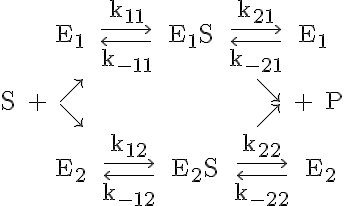
where k11 is the forward binding rate of S to E1, k-11 is the backwards reaction rate of E1S dissociating to E1 and S, k21 is the forward reaction rate of E1S forming E1 and P, k-21 is the reverse reaction rate of E1 and P producing E1S, k12 is the forward binding rate of S to E2, k-12 is the backwards reaction rate of E2S dissociating to E2 and S, k22 is the forward reaction rate of E2S forming E2 and P, and k-22 is the reverse reaction rate of E2 and P producing E2S.
Equations
This reaction is governed by a system of four ODEs which describe the concentrations of the substrate, enzyme complex for enzyme 1 and enzyme 2 and product. The fifth and sixth equations to close the system are given by specifying the total amount of enzyme 1, E1tot, and enzyme 2, E2tot present which must be conserved. The initial conditions specify that all of the substrate and no complex or product are present at time t=0. The system of equations are:
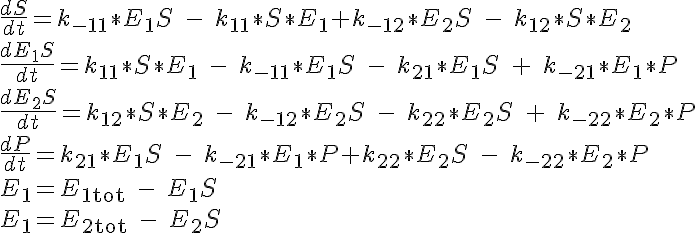
The backward reaction rates in this model are determined from the equilibrium dissociation rates of S and P binding to the enzymes and are given by:
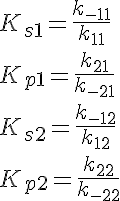
where Ks1 is the equilibrium dissociation rate of S binding to E1, Kp1 of P binding to E1, Ks2 of S binding to E2 and Kp2 of P binding to E2.
We welcome comments and feedback for this model. Please use the button below to send comments:
Bassingthwaighte JB.: Enzymes and Metabolic Reactions, Chapter 10 in
"Transport and Reactions in Biological Systems",
Please cite https://www.imagwiki.nibib.nih.gov/physiome in any publication for which this software is used and send one reprint to the address given below:
The National Simulation Resource, Director J. B. Bassingthwaighte, Department of Bioengineering, University of Washington, Seattle WA 98195-5061.
Model development and archiving support at https://www.imagwiki.nibib.nih.gov/physiome provided by the following grants: NIH U01HL122199 Analyzing the Cardiac Power Grid, 09/15/2015 - 05/31/2020, NIH/NIBIB BE08407 Software Integration, JSim and SBW 6/1/09-5/31/13; NIH/NHLBI T15 HL88516-01 Modeling for Heart, Lung and Blood: From Cell to Organ, 4/1/07-3/31/11; NSF BES-0506477 Adaptive Multi-Scale Model Simulation, 8/15/05-7/31/08; NIH/NHLBI R01 HL073598 Core 3: 3D Imaging and Computer Modeling of the Respiratory Tract, 9/1/04-8/31/09; as well as prior support from NIH/NCRR P41 RR01243 Simulation Resource in Circulatory Mass Transport and Exchange, 12/1/1980-11/30/01 and NIH/NIBIB R01 EB001973 JSim: A Simulation Analysis Platform, 3/1/02-2/28/07.

