This model shows the case of an enzyme facilitating the formation of a product from a substrate but an inhibitor exists which also can bind to the enzyme rendering it ineffective.
Description
This model represents the enzymatic conversion of a single substrate, S, to a single product, P, but there is an inhibitor, I, which also can bind to the enzyme, E, preventing it from forming the product. Initially the enzyme can either bind with the substrate forming the product yielding complex, ES, or it can bind to the inhibitor forming the non reacting complex, EI. If the ES complex is formed a reaction-release event follows, which yields the product and the enzyme. The entire binding- inhibition-reaction-release sequence may be represented symbolically as:
k1 --> k2 -->
S + I + E <-----------> ES <-----------> P + E
<-- k_1 <-- k_2
^
| | ^
k3 | | | k_3
v | |
v
EI
where k1 is the forward binding rate of S to E, k-1 is the backwards reaction rate of ES dissociating to E and S, k2 is the forward reaction rate of ES forming E and P, k-2 is the reverse reaction rate of E and P producing ES, k3 is the forward reaction rate of E binding to I and k-3 is the reaction rate of EI dissociating to form E and I.
Equations
This reaction is governed by a system of five ODEs which describe the concentrations of the substrate, inhibitor, enzyme complex ES, inhibition complex EI and product. The sixth equation to close the system specifies the total amount of enzyme present, Etot which must be conserved. All of the substrate and no complex or product are present at time t=0. The system of equations are:
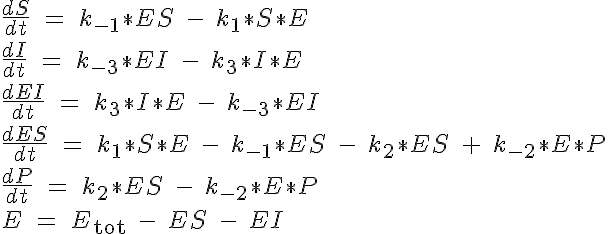
The backward reaction rates in this model are determined from the equilibrium dissociation rates of S binding to E, I binding to E and P binding to E. The expressions for the equilibrium dissociation rates are given by:
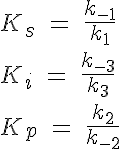
where Ks is the equilibrium dissociation rate of S binding to E, Ki of I binding to E and Kp of P binding to E. The reaction velocity is the current velocity of the reaction in forming the product, v, divided by the maximal reaction velocity, Vmax. If we assume Michaelis-Menten kinetics the reaction is rate limited by the dissociation of ES into E and P. Therefore we have:
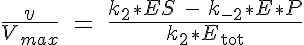
We welcome comments and feedback for this model. Please use the button below to send comments:
Segel IH.: "Enzyme Kinetics", John Wiley and Sons, New York, 1975, Chapter 3, Pages 100-112
Please cite https://www.imagwiki.nibib.nih.gov/physiome in any publication for which this software is used and send one reprint to the address given below:
The National Simulation Resource, Director J. B. Bassingthwaighte, Department of Bioengineering, University of Washington, Seattle WA 98195-5061.
Model development and archiving support at https://www.imagwiki.nibib.nih.gov/physiome provided by the following grants: NIH U01HL122199 Analyzing the Cardiac Power Grid, 09/15/2015 - 05/31/2020, NIH/NIBIB BE08407 Software Integration, JSim and SBW 6/1/09-5/31/13; NIH/NHLBI T15 HL88516-01 Modeling for Heart, Lung and Blood: From Cell to Organ, 4/1/07-3/31/11; NSF BES-0506477 Adaptive Multi-Scale Model Simulation, 8/15/05-7/31/08; NIH/NHLBI R01 HL073598 Core 3: 3D Imaging and Computer Modeling of the Respiratory Tract, 9/1/04-8/31/09; as well as prior support from NIH/NCRR P41 RR01243 Simulation Resource in Circulatory Mass Transport and Exchange, 12/1/1980-11/30/01 and NIH/NIBIB R01 EB001973 JSim: A Simulation Analysis Platform, 3/1/02-2/28/07.

