Permeability and reflection coefficient for a hard spherical solute, radius rs,through a cylindrical pore, radius rpore. Minimal code for Sigma and Perm; Hydrodynamic calculation from Bassingthwaighte 2006, corrected 2012

Description

   OBJECTIVE: The equations for transport of hydrophilic solutes through aqueous pores
   provide a fundamental basis for examining capillary-tissue exchange and water and
   solute flux through transmembrane channels, but the theory remains incomplete for
   ratios, alp, of sphere diameters to pore diameters greater than 0.4. Values for
   permeabilities, P, and reflection coefficients, sigma, from Lewellen [18], working
   with Lightfoot et al. [19], at alp = 0.5 and 0.95, were combined with earlier values
   for alp < 0.4, and the physically required alp < 1, to provide accurate expressions
   over the whole range of 0 < alp < 1. (alp =rs/rpore & stands for the greek alpha in the text.)

   METHODS: The "data" were the long-accepted theory for alp < 0.2 and the computational
   results from Lewellen and Lightfoot et al. on hard spheres (of 5 different alp's)
   moving by convection and diffusion through a tight cylindrical pore, accounting
   for molecular exclusion, viscous forces, pressure drop, torque and rotation of
   spheres off the center line (averaging across all accessible radial positions),
   and the asymptotic values at alp = 1.0. Coefficients for frictional hindrance to
   diffusion, F(alp), and drag, G(alp), and functions for sigma(alp) and P(alp), were
   represented by power law functions and the parameters optimized to give best
   fits to the combined "data".

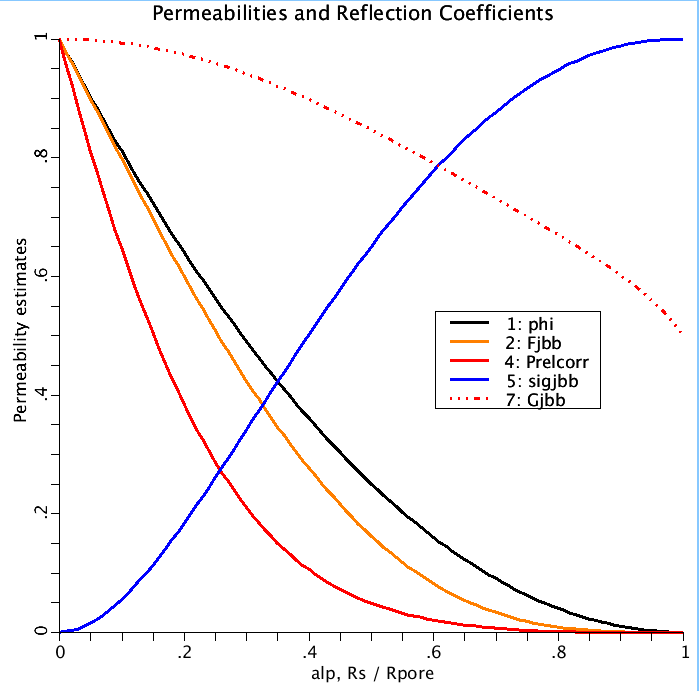
   RESULTS: The reflection coefficient sigma = {1 - (1 - (1-PHI)^2)*G'(alp)} + 2*alp^2*PHI*F'(alp),
   and the relative permeability P/Pmax = PHI*F'(alp)*(1 + 9* alp^5.5 * (1 -alp^5)^(0.02)],
   where PHI is the partition coefficient or volume fraction of the pore available to solute.
   The new expression for the diffusive hindrance is
   F'(alp) = (1-alp^2)^(3/2)*PHI / (1 + 0.2 alp^2 *(1 - alp^2)^16), and for the drag factor is
   G'(alp) = (1-(2/3)*alp^2 - 0.20217*alp^5) / (1 - 0.75851*alp^5) - 0.0431*[1 - (1 - alp^10)].
   All of these converge monotonically to the correct limits at alp = 1.

 CONCLUSION: These are the first expressions providing hydrodynamically based estimates
 of SIGMA(alp) and P(alp) over 0 < alp < 1. They should be accurate to within 1 to 2%.

Equations

The equations for this model may be viewed by running the JSim model applet and clicking on the Source tab at the bottom left of JSim's Run Time graphical user interface. The equations are written in JSim's Mathematical Modeling Language (MML). See the Introduction to MML and the MML Reference Manual. Additional documentation for MML can be found by using the search option at the Physiome home page.