Permeability and reflection coefficient for a hard spherical solute, radius rs,through a cylindrical pore, radius rpore. Hydrodynamic calculation from Bassingthwaighte 2006, corrected 2012
Description
OBJECTIVE: The equations for transport of hydrophilic solutes through aqueous pores
provide a fundamental basis for examining capillary-tissue exchange and water and
solute flux through transmembrane channels, but the theory remains incomplete for
ratios, alp, of sphere diameters to pore diameters greater than 0.4. Values for
permeabilities, P, and reflection coefficients, sigma, from Lewellen [18], working
with Lightfoot et al. [19], at alp = 0.5 and 0.95, were combined with earlier values
for alp < 0.4, and the physically required alp < 1, to provide accurate expressions
over the whole range of 0 < alp < 1. (alp =rs/rpore & stands for the greek alpha in the text.)
METHODS: The "data" were the long-accepted theory for alp < 0.2 and the computational
results from Lewellen and Lightfoot et al. on hard spheres (of 5 different alp's)
moving by convection and diffusion through a tight cylindrical pore, accounting
for molecular exclusion, viscous forces, pressure drop, torque and rotation of
spheres off the center line (averaging across all accessible radial positions),
and the asymptotic values at alp = 1.0. Coefficients for frictional hindrance to
diffusion, F(alp), and drag, G(alp), and functions for sigma(alp) and P(alp), were
represented by power law functions and the parameters optimized to give best
fits to the combined "data".
RESULTS: The reflection coefficient sigma = {1 - (1 - (1-PHI)^2)*G'(alp)} + 2*alp^2*PHI*F'(alp),
and the reloative permeabiltiy P/Omax = PHI*F'(alp)*(1 + 9* alp^5.5 * (1 -alp^5)^(0.02)],
where PHI is the partition coefficient or volume fraction of the pore available to solute.
The new expression for the diffusive hindrance is
F'(alp) = (1-alp^2)^(3/2)*PHI / (1 + 0.2 alp^2 *(1 - alp^2)^16), and for the drag factor is
G'(alp) = (1-(2/3)*alp^2 - 0.20217*alp^5) / (1 - 0.75851*alp^5) - 0.0431*[1 - (1 - alp^10)].
All of these converge monotonically to the correct limits at alp = 1.
CONCLUSION: These are the first expressions providing hydrodynamically based estimates
of SIGMA(alp) and P(alp) over 0 < alp < 1. They should be accurate to within 1 t0 2%.
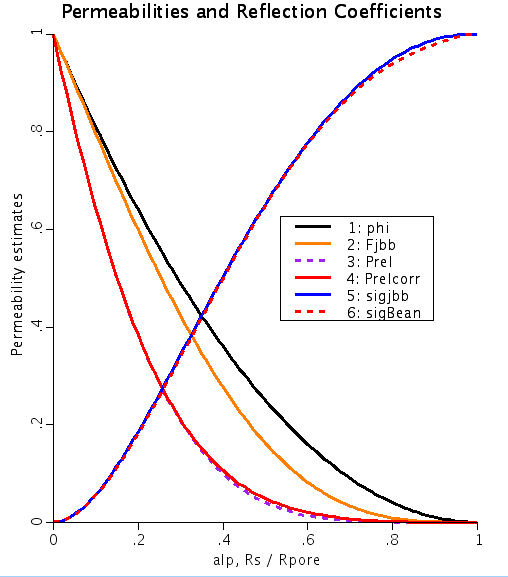
Figure: Permeabilities and reflection coefficients as a function of alp, the ratio of solute radius to pore radius. phi is the solute partition coeffecient, Fjbb is the new fractional hindrance factor, Prel is Relative pore permeability due to exclusion, Prelcorr is the ratio of pore permeability to maximum pore permeability, sigjbb is the new reflection coefficient and sigBean is Bean's calculation of the reflection coefficient. Parameter set 'Par1' of JSim model PoreTransport.proj was used to obtain the above figure.
Equations
The equations for this model may be viewed by running the JSim model applet and clicking on the Source tab at the bottom left of JSim's Run Time graphical user interface. The equations are written in JSim's Mathematical Modeling Language (MML). See the Introduction to MML and the MML Reference Manual. Additional documentation for MML can be found by using the search option at the Physiome home page.
- Download JSim model MML code (text):
- Download translated SBML version of model (if available):
We welcome comments and feedback for this model. Please use the button below to send comments:
Bassingthwaighte JB. A practical extension of hydrodynamic theory of porous transport for hydrophilic solutes. Microcirculation 13: 111-118, 2006. (#591) Bassingthwaighte JB. Erratum to: A practical extension of hydrodynamic theory of porous transport for hydrophilic solutes. Microcirculation 19(7): 668, 2012. (#650) -corrected Eq 12 to use +16/9 * rather than -16/9 *. and curve for Bean in Fig 3. Apelblat A, Katzir-Katchalsky A, and Silberberg A. A mathematical analysis of capillary-tissue fluid exchange. Biorheology 11: 1-49, 1974. Bean CP. The physics of porous membranes: neutral pores. In: Membranes: Macroscopic Systems and Models, edited by Einsenman G. New York: Dekker, 1972, p. 1-54 Biber TUL and Curran PF. Coupled solute fluxes in toad skin. J Gen Physiol 51: 606-620, 1968. Curry FE. Mechanics and thermodynamics of transcapillary exchange.. In: Handbook of Physiology, Sec. 2 The Cardiovascular System. Vol. 4, Microcirculation, edited by Renkin EM and Michel CC. American Physiological Society: Bethesda, Maryland, 1984, p. 309-374. Ginzburg BZ and Katchalsky A. The frictional coefficients of the flows of non-electrolytes through artificial membranes. J Gen Physiol 47: 403-418, 1963. Katchalsky A and Curran PF. Nonequilibrium Thermodynamics in Biophysics. Cambridge, MA: Harvard University Press, 1965. Kedem O and Katchalsky A. Thermodynamic analysis of the permeability of biological membranes to non-electrolytes. Biochim Biophys Acta 27: 229-246, 1958. Kedem O and Katchalsky A. A physical interpretation of the phenomenological coefficients of membrane permeability. J Gen Physiol 45: 143-179, 1961. Kellen MR and Bassingthwaighte JB. An integrative model of coupled water and solute exchange in the heart. Am J Physiol Heart Circ Physiol 285: H1303-H1316, 2003. Kellen MR and Bassingthwaighte JB. Transient transcapillary exchange of water driven by osmotic forces in the heart. Am J Physiol Heart Circ Physiol 285: H1317-H1331, 2003. Lewellen PC. Hydrodynamic Analysis of Microporous Mass Transport. Ph.D. Thesis, University of Wisconsin-Madison (1982). Lewellen PC, Bassingthwaighte JB, Lightfoot EN, and Stewart WE. Microporous membrane transport. Microvasc Res 25: 245, 1983. (#195) Lightfoot EB, Bassingthwaighte JB, Grabowski EF, Hydrodynamic models for diffusion in microporous membranes. Ann Biomed Eng 4:78-90 (1976). (#130)
Please cite https://www.imagwiki.nibib.nih.gov/physiome in any publication for which this software is used and send one reprint to the address given below:
The National Simulation Resource, Director J. B. Bassingthwaighte, Department of Bioengineering, University of Washington, Seattle WA 98195-5061.
Model development and archiving support at https://www.imagwiki.nibib.nih.gov/physiome provided by the following grants: NIH U01HL122199 Analyzing the Cardiac Power Grid, 09/15/2015 - 05/31/2020, NIH/NIBIB BE08407 Software Integration, JSim and SBW 6/1/09-5/31/13; NIH/NHLBI T15 HL88516-01 Modeling for Heart, Lung and Blood: From Cell to Organ, 4/1/07-3/31/11; NSF BES-0506477 Adaptive Multi-Scale Model Simulation, 8/15/05-7/31/08; NIH/NHLBI R01 HL073598 Core 3: 3D Imaging and Computer Modeling of the Respiratory Tract, 9/1/04-8/31/09; as well as prior support from NIH/NCRR P41 RR01243 Simulation Resource in Circulatory Mass Transport and Exchange, 12/1/1980-11/30/01 and NIH/NIBIB R01 EB001973 JSim: A Simulation Analysis Platform, 3/1/02-2/28/07.

