A model for the dynamics of human weight cycling based on the work of Albert Goldbeter [J. Biosci, 31, 129-136] and presented by Lauren Shepherd as a final project for BIOEN 589, University of Washington.

Description

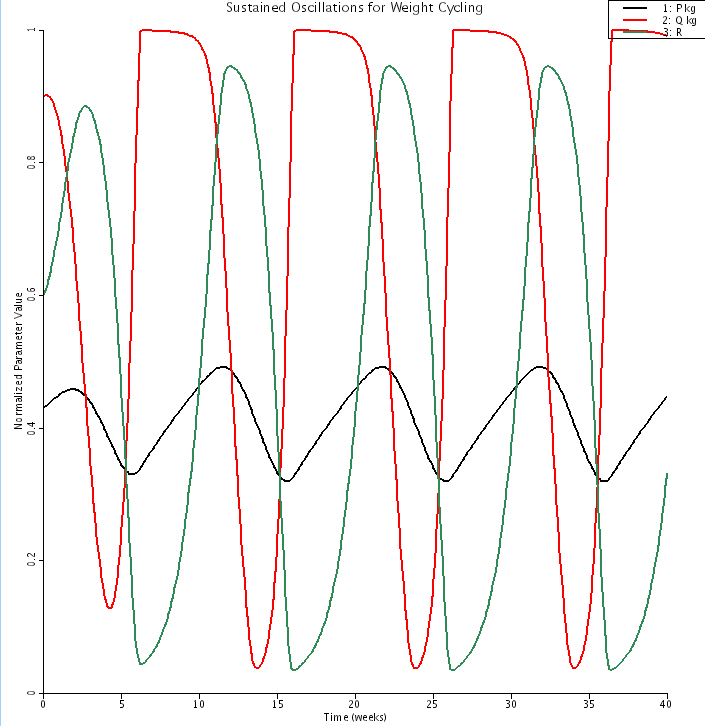
 The resolution to lose weight by cognitive restraint of nutritional intake often leads 
 to repeated bouts of weight loss and regain, a phenomenon known as weight cycling or “yo-yo 
 dieting.” A simple mathematical model for weight cycling is presented. The model is based 
 on a feedback of psychological nature by which a subject decides to reduce dietary intake 
 once a threshold is exceeded. The analysis of the model indicates that sustained oscillations 
 in body weight occur in a parameter range bounded by critical values. Only outside this range 
 can body weight reach a stable steady state. The model provides a theoretical framework that 
 captures key facets of weight cycling and suggests ways to control the phenomenon. 
 The view that weight cycling represents self-sustained oscillations has indeed specific 
 implications. In dynamical terms, to bring weight cycling to an end, parameter values should 
 change in such a way as to induce the transition of body weight from sustained oscillations 
 around an unstable steady state to a stable steady state. Maintaining weight under a critical 
 value should prevent weight cycling and allow body weight to stabilize below the oscillatory 
 range. 	

 The original model was changed by Lauren Shepherd to allow exploration of the effects of 
 metabolic changes over time. The static parameter 'a' (metabolic efficiency) was turned into 
 a linear function that slowly increases with time. To activate this part of the code, enter 
 '2' as the value for the 'ab' parameter. Under these conditions, the oscillatory behavior 
 still exists, but the maximum body weight continues to climb over time.

 A second change can be made by altering the energy dissipation parameter 'b'. To activate 
 this change, enter '3' as the value for the 'ab' parameter. A body weight decrease will be 
 observed with this metabolic change.

• Commentary on model by Lauren Shepherd (Word doc)25.5 KB

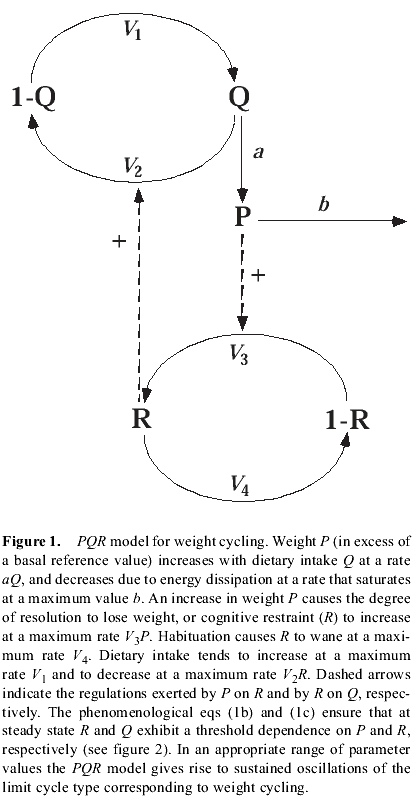
Equations

Calculation of the Threshold Values:

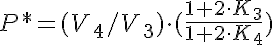
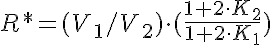
ODE System:

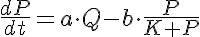
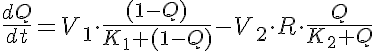
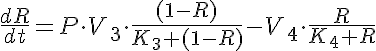
The equations for this model may be viewed by running the JSim model applet and clicking on the Source tab at the bottom left of JSim's Run Time graphical user interface. The equations are written in JSim's Mathematical Modeling Language (MML). See the Introduction to MML and the MML Reference Manual. Additional documentation for MML can be found by using the search option at the Physiome home page.