An axially-distributed facilitating transporter for two competing solutes, A and B, including binding steps, with input via flow. Shows countertransport facilitation/inhibition. There is Enzymatic conversion A -> B in V2.
Figure
The input function Ain(t) = 1 mM, a constant. Solute A is transported from V1 to V2 by a transporter that can bind to either A or B. The transporter can flip from side to side in the unbound form T, or in the bound forms, TA and TB. In V2, A is converted to B by a saturable Michaelis-Menten process.
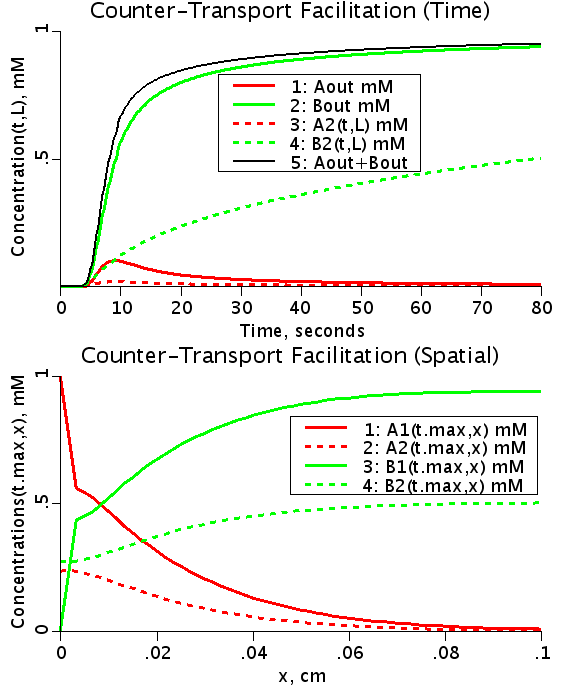
When the rate of flipping as unbound transporter, T1 and T2, is less than the rate for the bound transporter, TA1, TB1, TA2, and TB2, then the presence of B in V2 facilitates the transfer of A from V1 to V2 because it makes more unbound T1 on side 1 than if there were no B in V2. This can be seen by the increase in transmembrane extraction of A after 35-45 seconds when B2 has built up enough TB2 and TB1, which then delivers B to V1 giving more unbound T1 so A1 diminishes.
Description
This is a 1-D two region model separated by a membrane. The model includes flow, exchange, axial diffusion, consumption, and an enzymatic reaction for two metabolites. Units are given as "per gram of tissue", adhering to pysiological nomenclature.
Exchange between the two regions occurs via two parallel routes:
(1) Passive exchange between the two regions governed by the parameters PSa and PSb which mediate the exchange for solutes A and B respectively;
(2) T1-T2 facilitated competitive transport through the membrane between the two regions.
A Michaelis-Menten uni-directional reaction converts solute A to solute B in the non-flowing region.
Note that the equations for the transporter moities include a diffusive term with a zero diffusion coefficient. This is necessary for correct sequencing of calculations so that all equations are included in the partial differential equation solver.
Equations
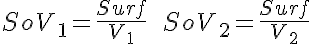
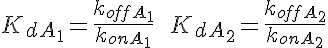
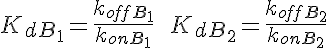
Partial Differential Equations
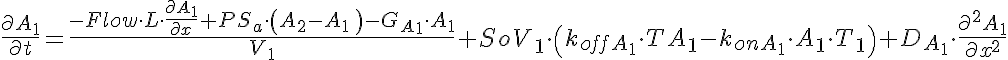
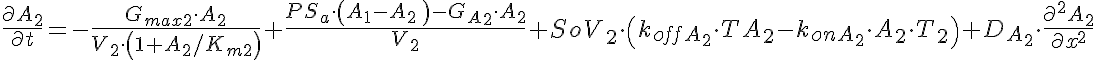
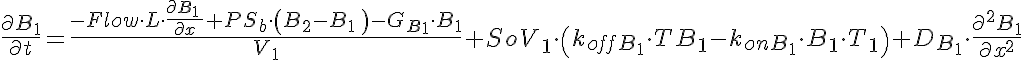
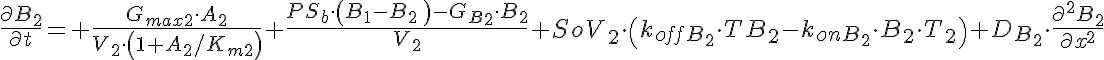
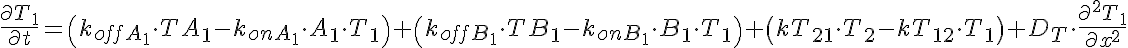
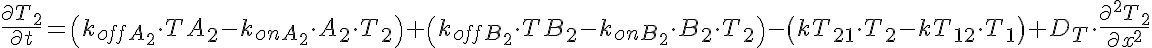
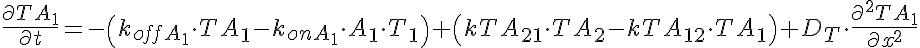
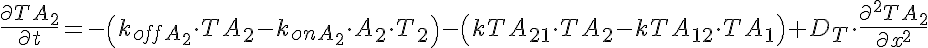
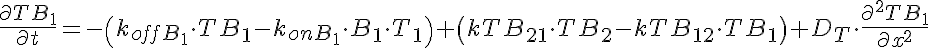
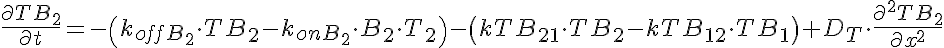
Transporter Mass Conservation
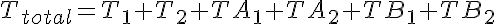
Substrate Mass Conservation
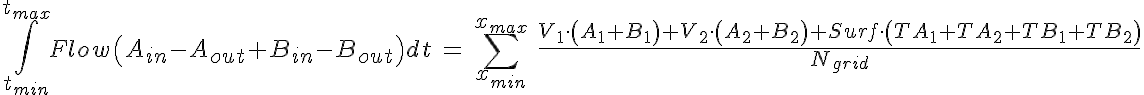
WARNING: Thermodynamic constraint are not included in the model. For a passive transporter, the transport rate constants should satisfy the following constraints:
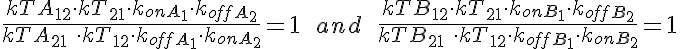
The equations for this model may be viewed by running the JSim model applet and clicking on the Source tab at the bottom left of JSim's Run Time graphical user interface. The equations are written in JSim's Mathematical Modeling Language (MML). See the Introduction to MML and the MML Reference Manual. Additional documentation for MML can be found by using the search option at the Physiome home page.
- Download JSim model MML code (text):
- Download translated SBML version of model (if available):
- No SBML translation currently available.
- Information on SBML conversion in JSim
We welcome comments and feedback for this model. Please use the button below to send comments:
Sangren WC and Sheppard CW. A mathematical derivation of the exchange of a labeled substance between a liquid flowing in a vessel and an external compartment. Bull Math Biophys 15: 387-394, 1953 (This gives an analytic solution for the two-region model.) Goresky CA, Ziegler WH, and Bach GG. Capillary exchange modeling: Barrier-limited and flow-limited distribution. Circ Res 27: 739-764, 1970. (This gives another derivation of the analytical form, and uses the model in both single and multicapillary models. Bassingthwaighte JB. A concurrent flow model for extraction during transcapillary passage. Circ Res 35: 483-503, 1974. (This gives numerical solutions, which are faster than the analytic solutions, and imbeds the model in an organ with tissue volums conserved, and with arteries and veins. The original Lagrangian sliding fluid element model with diffusion.) Guller B, Yipintsoi T, Orvis AL, and Bassingthwaighte JB. Myocardial sodium extraction at varied coronary flows in the dog: Estimation of capillary permeability by residue and outflow detection. Circ Res 37: 359-378, 1975. (Application to sodium exchange in the heart.) Goresky CA. Hepatic membrane carrier transport processes: Their involvement in bilirubin uptake. In: Chemistry and Physiology of Bile Pigments. Washington, D.C.: Publishing House U.S. Government, 1977, p. 265-281. Silverman M and Goresky CA. A unified kinetic hypothesis of carrier-mediated transport: Its applications. Biophys J 5: 487-509, 1965.
Please cite https://www.imagwiki.nibib.nih.gov/physiome in any publication for which this software is used and send one reprint to the address given below:
The National Simulation Resource, Director J. B. Bassingthwaighte, Department of Bioengineering, University of Washington, Seattle WA 98195-5061.
Model development and archiving support at https://www.imagwiki.nibib.nih.gov/physiome provided by the following grants: NIH U01HL122199 Analyzing the Cardiac Power Grid, 09/15/2015 - 05/31/2020, NIH/NIBIB BE08407 Software Integration, JSim and SBW 6/1/09-5/31/13; NIH/NHLBI T15 HL88516-01 Modeling for Heart, Lung and Blood: From Cell to Organ, 4/1/07-3/31/11; NSF BES-0506477 Adaptive Multi-Scale Model Simulation, 8/15/05-7/31/08; NIH/NHLBI R01 HL073598 Core 3: 3D Imaging and Computer Modeling of the Respiratory Tract, 9/1/04-8/31/09; as well as prior support from NIH/NCRR P41 RR01243 Simulation Resource in Circulatory Mass Transport and Exchange, 12/1/1980-11/30/01 and NIH/NIBIB R01 EB001973 JSim: A Simulation Analysis Platform, 3/1/02-2/28/07.

