Barrier-limited model of Goresky, using Finite difference method

Theory

Single capillary

The concentrations in plasma, C₁ and in tissue, C₂, follow the following system of two differential equations in time, t, and space, x:

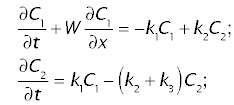
where W is the linear velocity of the tracer the sinusoidal plasma, k₁ and k₂ are transfer coefficients or rate constants, defining the transfer of tracer between the plasma and tissue, and k₃ is the transfer coefficient of sequestration of tracer due to metabolism and/or biliary excretion.

The boundary conditions are

• at t = 0: C₁ = 0 and C₂ = 0;
• at x = 0: C₁ = C_in

where C_in is the tracer concentration at the inflow of the organ. For quasi-instantaneuse injection, administration of tracer will be represented by the Dirac impulse function: C_in(t) = δ(t). In order to make calculations easier, concentrations are normalized by dividing through the injected amount, and distances are normalized by dividing through the linear velocity W, thus assuiming W = 1.

Whole organ

The tracer concentration leaving the whole organ, C_diff, is obtained as the flow-weighted average of the cocentration in the individual sinusoids. Let f(τ_c) be the fraction of total organ blood flow emerging from paths with sinusoidal transit times between τ_c and τ_c + dτ_c. The mixed outflow concentration from the whole organ, C(t), will then be the flow-weighted average of the outflow concentrations, according to the integral

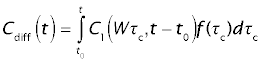
For the reference tracer (sucrose), the normalized concentration at the portal vein is

C_ref = f(τ_c + t₀)

Thus,

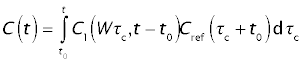
Closed solution

The closed ("analytical") solution for the whole-organ response is

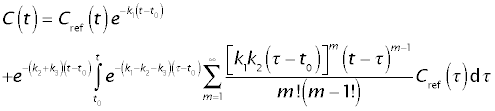
The solution consists of two components:

1. The throughput component, e^{-k₁(t - t₀)} C_ref(t), representing tracer that remained in the extracellular space.
2. The returning component, repesented by the second line of the above equation, representing tracer that has entered the tissue at least one and has returned to the extracellular space.

Calculations

Parameter sets

There are five parameter sets in this JSim model project file:

• Gal1: Galactose experiment with no galactose infused
• Gal2: Galactose experiment with high galactpse concentration
• Pal1: Palmitate acid experiment (normal control)
• Pal2: Palmitate acid experiment with infusion of α-bromopalmitate
• Rb: Rubidium experiment

To change the parameter set:

1. Select Load project parameter set from the ParSet pulldown menu
2. Choose the desired parameter set. This will automatically change the paremters as well as the data for the reference curve.
3. Click on "Run" to use the new parameter set.
4. In order to show the correct data in the plot, select the data set and the tracer from the pulldown menus labeled "data".

Closed solution

Select model "ClosSol" from the pulldown menu activated by the "Models" tab. Notice that the calcuation using the closed solution is much faster than the finite-different caculation. The parameter set has to be changed separately for each calculation method.

Optimization

If you want to optimize the parameters of the newly selected experiments

1. Click on the Optimizer tab (at the bottom of the left pane)
2. Change all the DataSet entries under the "Data to Match" heading.
   • Click on the Dataset entries to get a selection of data sets to choose from.
   • Click on the Curve entries to get a selection of data columns to choose from.
3. Hit the "Run" button.