Facilitating Transporter for 2 competing solutes including binding steps. Shows countertransport facilitation/inhibition. Substrate A is converted to B in region 2.

Figure

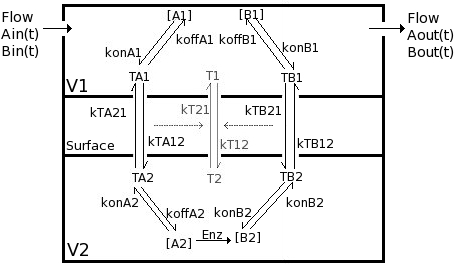
The input function Ain(t) = 1 mM, a constant. Solute A is transported from V1 to V2 by a transporter that can bind to either A or B. The transporter can flip from side to side in the unbound form T, or in the bound forms, TA and TB. In V2, A is converted to B by an irreversible Michaelis-Menten like process.

When the rate of flipping of the unbound transporter, T1 to T2 and vice versa, is less than the rate for the bound transporter, TA1, TB1, TA2, and TB2, then the presence of B2 in V2 facilitates the transfer of A from V1 to V2 because it augments the return into unbound T1 on side 1. This can be seen by the increase in transmembrane flux of A after 35-45 seconds when B2 has built up enough TB2 and TB1, which then delivers B to V1 giving more unbound T1 so A1 diminishes.

Description

  Transp2sol.Comp2F is a six state transporter model for 2 solutes in competition
  Two solute species compete for the transporter site on either side of a
  membrane between two mixing chambers. In compartment 2, A is reacted to form B
  in an enzymatic reaction approximated by a Michaelis Menten expression, 
  and without any accounting for binding of substrate or product to the 
  enzyme. When the rates of conformational state change for transmembrane 
  flipping of TA and TB are high compared to that for uncomplexed transporter T,
  then the model behaves much like an obligatory countertransporter, exchanging
  B for A across the membrane; With the initial substrate concentrations high
  compared to the transporter binding affinities, KdA or KdB, most of the
  transporter is bound and the system behaves as an obligatory countertransporter,
  though the gradient eventually dissipates.

  MODEL VERIFICATION: Total Mass is conserved: Substrate in solution is
  totaled as SubstrateV, and substrate bound to transporter as SubstrateM, 
  for membrane bound. 

Equations

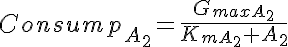
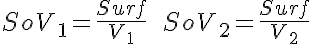
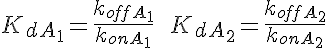
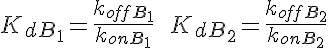
     Ordinary Differential Equations

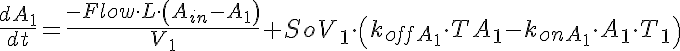
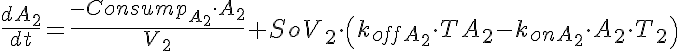
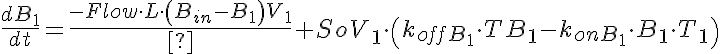
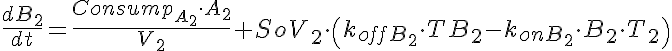
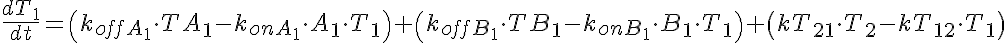
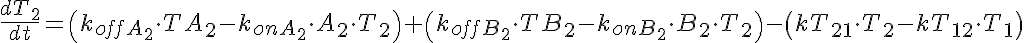
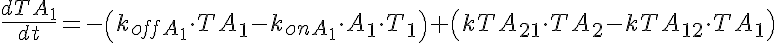
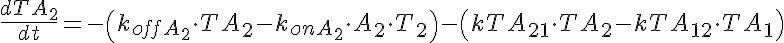
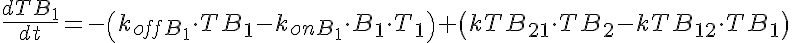
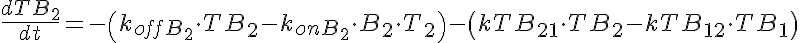
     Transporter Mass Conservation

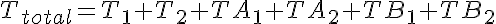
     Substrate Mass Conservation

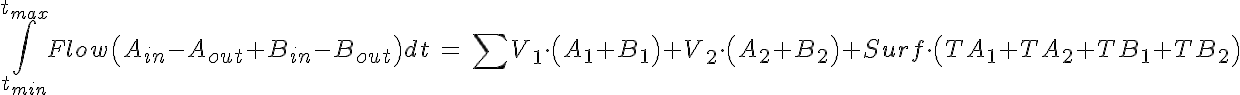
WARNING: Thermodynamic constraint are not included in the model. For a passive transporter, the transport rate constants should satisfy the following constraints:

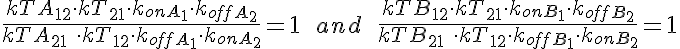
The equations for this model may be viewed by running the JSim model applet and clicking on the Source tab at the bottom left of JSim's Run Time graphical user interface. The equations are written in JSim's Mathematical Modeling Language (MML). See the Introduction to MML and the MML Reference Manual. Additional documentation for MML can be found by using the search option at the Physiome home page.