Generate a 2-D fractional Brownian motion walk using the the Davies-Harte algorithm. (see FGP, model 346 for details).
Description
The Davies-Harte algorithm is used to generate fractional Gaussian noise (fGn) and
fractional Brownian Motion (fBm). The algorithm is described in model #346 and is
named FGP (Fractional Gaussian Process). Two copies of the algorithm
are employed here, one for the x increments and one for the y increments.
Two copies were employed so that the X and Y increments would be independent of
each other.
The relationship between fBm and fGn is given by
m
-----
\
fBm(m) = ) fGn(j), for m=0 to N.
/
-----
j = 0
The JSim project contains the following plots run with the default parameter set
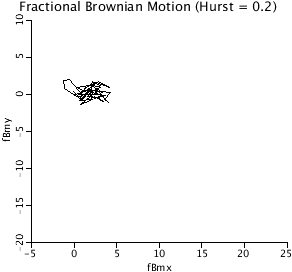
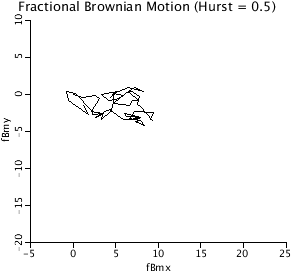
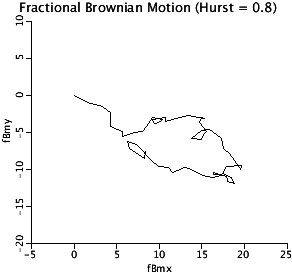
DBM2D: The 2-D plot of fractional Brownian Motion,
FBMX_and_FBYM: Plots of the x-traces and y-traces for the 1-D fractional
Brownian Motions for X and Y and the fractional Gaussian noise
(fGn) increments that are summed to produce the fBm.
GaussianIncrements: The fGn series are sorted in ascending order and plotted as
(m/m.max, sorted fGn(m)) where m runs from 1 to m.max. This
demonstrates that the increments are Gaussian. For Hurst
coefficients > 0.5, each individual realization can depart
from Gaussian.
There are two nested plot plots run with the correlationfGnRunLoops parameter set.
The user should load that parameter set and run loops. The two plots are:
fGn_correl: Shows that for Hurst coefficients <0.5, adjacent points are
likely to be negatively correlated, while for Hurst
coefficients >0.5, adjacent points are more likely to be
positively correlated.
fGnx_fGny_Xcorrel: Shows that for an individual realization, the fGnx and the
fGny are independent of each other.
CAVEAT: Model is slow for Npoints >2,000 as the Fourier transforms used
here are not the complex Fast Fourier Transforms. The code utilizes
discrete cosine and sine transforms and treats all quantities as
real variables because JSim does not support complex variables and
the FFT cannot be written as a single simple equation.
Equations
None.
The equations for this model may be viewed by running the JSim model applet and clicking on the Source tab at the bottom left of JSim's Run Time graphical user interface. The equations are written in JSim's Mathematical Modeling Language (MML). See the Introduction to MML and the MML Reference Manual. Additional documentation for MML can be found by using the search option at the Physiome home page.
- Download JSim model MML code (text):
- Download translated SBML version of model (if available):
We welcome comments and feedback for this model. Please use the button below to send comments:
Davies, RB and Harte DS. Tests for the Hurst Effect, Biometrica 74 (1987), 95-101.
Fractal Models
Please cite https://www.imagwiki.nibib.nih.gov/physiome in any publication for which this software is used and send one reprint to the address given below:
The National Simulation Resource, Director J. B. Bassingthwaighte, Department of Bioengineering, University of Washington, Seattle WA 98195-5061.
Model development and archiving support at https://www.imagwiki.nibib.nih.gov/physiome provided by the following grants: NIH U01HL122199 Analyzing the Cardiac Power Grid, 09/15/2015 - 05/31/2020, NIH/NIBIB BE08407 Software Integration, JSim and SBW 6/1/09-5/31/13; NIH/NHLBI T15 HL88516-01 Modeling for Heart, Lung and Blood: From Cell to Organ, 4/1/07-3/31/11; NSF BES-0506477 Adaptive Multi-Scale Model Simulation, 8/15/05-7/31/08; NIH/NHLBI R01 HL073598 Core 3: 3D Imaging and Computer Modeling of the Respiratory Tract, 9/1/04-8/31/09; as well as prior support from NIH/NCRR P41 RR01243 Simulation Resource in Circulatory Mass Transport and Exchange, 12/1/1980-11/30/01 and NIH/NIBIB R01 EB001973 JSim: A Simulation Analysis Platform, 3/1/02-2/28/07.

