Generate a 2-D fractional Brownian motion walk using the the Davies-Harte algorithm. (see FGP, model 346 for details).

Description

The Davies-Harte algorithm is used to generate fractional Gaussian noise (fGn) and
fractional Brownian Motion (fBm). The algorithm is described in model #346 and is
named FGP (Fractional Gaussian Process). Two copies of the algorithm
are employed here, one for the x increments and one for the y increments.
Two copies were employed so that the X and Y increments would be independent of
each other.

The relationship between fBm and fGn is given by 

                                         m
                                      -----
                                       \
                             fBm(m) =   )   fGn(j),  for m=0 to N.
                                       /
                                      -----
                                      j = 0



The JSim project contains the following plots run with the default parameter set
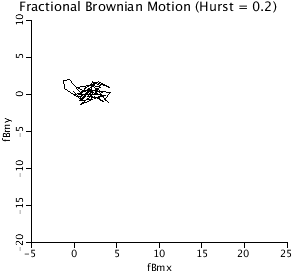
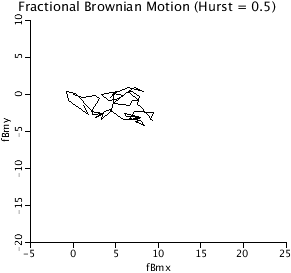
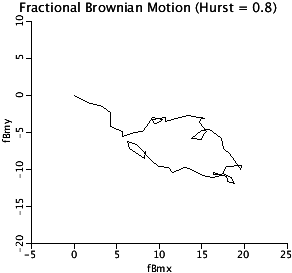
DBM2D:              The 2-D plot of fractional Brownian Motion,
FBMX_and_FBYM:      Plots of the x-traces and y-traces for the 1-D fractional 
                    Brownian Motions for X and Y and the fractional Gaussian noise 
                    (fGn) increments that are summed to produce the fBm.
GaussianIncrements: The fGn series are sorted in ascending order and plotted as
                    (m/m.max, sorted fGn(m)) where m runs from 1 to m.max. This
                    demonstrates that the increments are Gaussian. For Hurst
                    coefficients > 0.5, each individual realization can depart
                    from Gaussian.

There are two nested plot plots run with the correlationfGnRunLoops parameter set.
The user should load that parameter set and run loops. The two plots are:
fGn_correl:         Shows that for Hurst coefficients <0.5, adjacent points are
                    likely to be negatively correlated, while for Hurst 
                    coefficients >0.5, adjacent points are more likely to be 
                    positively correlated.
fGnx_fGny_Xcorrel:  Shows that for an individual realization, the fGnx and the 
                    fGny are independent of each other.


CAVEAT: Model is slow for Npoints >2,000 as the Fourier transforms used
       here are not the complex Fast Fourier Transforms. The code utilizes
       discrete cosine and sine transforms and treats all quantities as
       real variables because JSim does not support complex variables and
       the FFT cannot be written as a single simple equation.

Equations

None.

The equations for this model may be viewed by running the JSim model applet and clicking on the Source tab at the bottom left of JSim's Run Time graphical user interface. The equations are written in JSim's Mathematical Modeling Language (MML). See the Introduction to MML and the MML Reference Manual. Additional documentation for MML can be found by using the search option at the Physiome home page.