Uncoupled, independent fluxes of water and of 2 solutes, across a membrane separating 2 stirred tanks equipped with columns above each to provide observable column heights as measures of their pressures.
Description
This model is the same as Osm.Uncoupled1.proj except for using column heights
instead of elasticity. It also allows temperature changes.
Uncoupled, independent fluxes of water and of 2 solutes,
A and B, across a membrane separating 2 stirred tanks. Solute activities
are assumed unity so concentrations = thermodynamic activity. The model describes
a situation similar to that for the simplest expressions of Kedem and Katchalsky
(1958) but omits all interactions between solutes and between water and
any solute. One can think of the solutes passing though the membrane by
passive permeation with permeability coefficients PermA and Perm B, and
the water passing through aqueous pores with filtration coefficient or
hydraulic conductivity, Lp. The aqueous pores do not permit solute passage.
Lp is the same as the traditional filtration coefficient Kf. Lp translates
to a conventional permeability for water filtration, Pf cm/s,
Pf = Lp*RT/Vw
where RT = 19.347*10^6 mmHg*cm^3*mol^(-1) at 37C, Vw is the partial molar volume
of water, 18 ml/mol or the concentration of water in water is 55.55 M
The driving forces are the pressure difference for water flux and the
concentration for the solute fluxes. The pressure difference across the
membrane is the hydrostatic pressure difference minus the osmotic pressure
difference. The osmotic pressure is given by Van't Hoff's Eq:
p_osm = a.C.RT, where p_osm is the osmotic pressure, mmHg,
"a" is the activity coefficient, assumed in this model to equal unity,
C is concentration, M, and RT is the Gas Constant times Temperature Kelvin.
In this model the solute doesn't permeate the aqueous pore so there is
no consideration of a reflection coefficient, or rather it is assumed to be unity.
Thus solute concentration in the pore water is zero, and there is no solute advection..
The system is composed of two volumes of pressure-dependent size, yet
stirred instantaneously continually. The slope of the pressure/volume
relationship is linear and defined by the height of a column of fluid above
the rigid chambers The narrow columns of fluid have heights h1 and h2.
The pressure is rho*grav*h1 in chamber 1, where rho is fluid density,
grav is acceleration due to gravity;
The fluid in the columns is considered to be instantaneously mixed with that
in the chamber from which it rises. Fluid or volume flux, Jv, from side 1 to
side 2 causes a difference in the column heighta between the two sides by
Base*(h2-h1) = Jv, where Base = area of the base of the column, and the
pressure difference rises to rho* grav*(h2-h1) cm H2O, where rho is the fluid
density. g/ml, in the narrow colums..
The model OsmUncoupledA.proj uses an analogous linear chamber elastance, Elast mmHg/ml,
gives an equivalent measure for flexible chambers, assuming a linear relationship between
the pressure change and the volume change. (1 mmHg = 13.59 cm H2O.)
Notes: Situation 1:= Model default par. . PermA = 0, PermB > 0.1. See Notes.
Situation 2 = Model par2 PermB > 0.
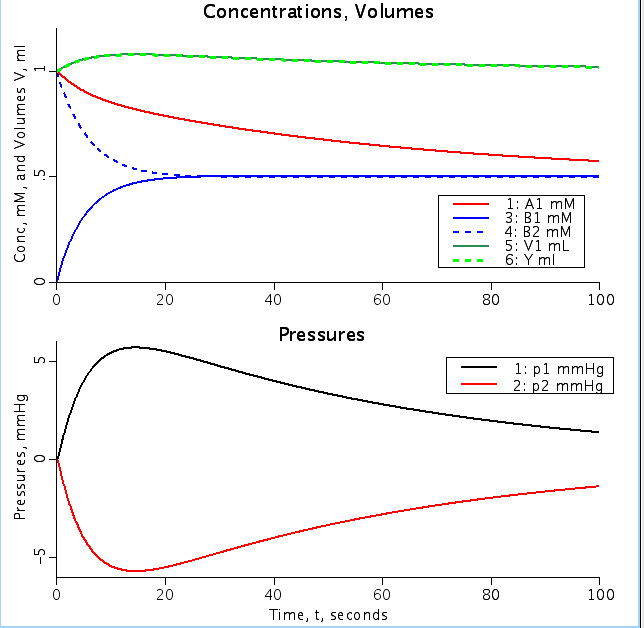
Figure: Top shows concentration of solute A and solute B as a function of time (A1, B1: conc in volume 1, A2, B2 conc in volume 2). Note change in volume 1 (V1) from initial volume of 1 ml. Y is volume 1 calculated from the membrane permeability while V1 is calculated from Hydraulic conductivity. Bottom figure shows hydrostatic pressure in V1 and volume 2 (V2) as a function of time. Permeability of A into V2 is one tenth the permeability of B and A2init and B1init are 0 mM for both figures.
Equations
The equations for this model may be viewed by running the JSim model applet and clicking on the Source tab at the bottom left of JSim's Run Time graphical user interface. The equations are written in JSim's Mathematical Modeling Language (MML). See the Introduction to MML and the MML Reference Manual. Additional documentation for MML can be found by using the search option at the Physiome home page.
- Download JSim model MML code (text):
- Download translated SBML version of model (if available):
We welcome comments and feedback for this model. Please use the button below to send comments:
Katchalsky A and Curran PF. Nonequilibrium Thermodynamics in Biophysics. Cambridge, MA: Harvard University Press, 1965. Kedem O and Katchalsky A. Thermodynamic analysis of the permeability of biological membranes to non-electrolytes. Biochim Biophys Acta 27: 229-246, 1958. Stein WD. The Movement of Molecules across Cell Membranes. New York: Academic Press, 1967. Stein WD. Transport and Diffusion across Cell Membranes. Orlando, Florida: Academic Press Inc., 1986.
Please cite https://www.imagwiki.nibib.nih.gov/physiome in any publication for which this software is used and send one reprint to the address given below:
The National Simulation Resource, Director J. B. Bassingthwaighte, Department of Bioengineering, University of Washington, Seattle WA 98195-5061.
Model development and archiving support at https://www.imagwiki.nibib.nih.gov/physiome provided by the following grants: NIH U01HL122199 Analyzing the Cardiac Power Grid, 09/15/2015 - 05/31/2020, NIH/NIBIB BE08407 Software Integration, JSim and SBW 6/1/09-5/31/13; NIH/NHLBI T15 HL88516-01 Modeling for Heart, Lung and Blood: From Cell to Organ, 4/1/07-3/31/11; NSF BES-0506477 Adaptive Multi-Scale Model Simulation, 8/15/05-7/31/08; NIH/NHLBI R01 HL073598 Core 3: 3D Imaging and Computer Modeling of the Respiratory Tract, 9/1/04-8/31/09; as well as prior support from NIH/NCRR P41 RR01243 Simulation Resource in Circulatory Mass Transport and Exchange, 12/1/1980-11/30/01 and NIH/NIBIB R01 EB001973 JSim: A Simulation Analysis Platform, 3/1/02-2/28/07.

